微积分02:极限

前言

由中学的数学跨入大学数学，有一个最直观的感受便是，由原来研究静态变量关系，变成了动态的了，这个将会贯穿学习微积分的始终。

极限的基本概念

极限是描述函数一个定点的行为，极限是指某个变量，不断接近于某个数值，但又不等于这个数值，它始终都是在小于这个数值的范围内波动，我们把这个数值就称为另一个变量的极限。例如我们写一个f(x)=x-1，x趋于2的极限等于1的式子，记作:。

左极限、右极限、双侧极限

用数学语言的表示方式：

如果左右极限互不相等，则表示为：

函数的渐近线

一个函数的确可以有不同的右侧和左侧水平渐近线，但最多只能有两条水平渐近线（一条在右侧，另一条在左侧）．它也有可能一条都没有，或者只有一条。一个函数不可能和它的渐近线相交

函数极限

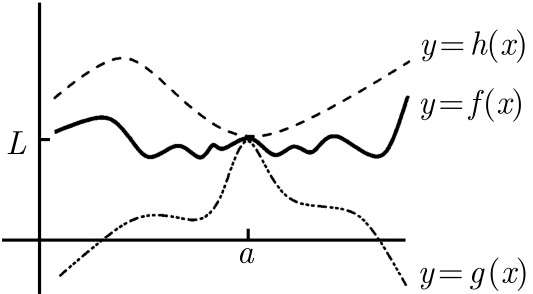
三明治法则（夹逼定理）

概念：如果一个函数f被夹在函数g和h之间，当x→a时，这两个函数g和h都收敛于同一个极限L，那么当x→a时，f也收敛于极限L。夹逼定理就是说在a附近的x都有：且

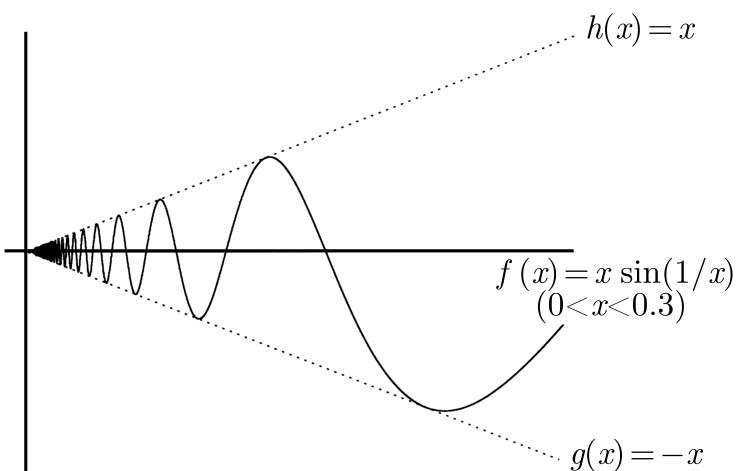
示例

例题

小结

具有代表类型的图像

1、当x=a时的右极限，此时在x=a的左侧以及x=a处于f(x)的行为是无关紧要的，换句话说当讨论右极限时，对于x≤a，f(x)取何值都不要紧。x≤a，f(x)甚至都不需要被定义

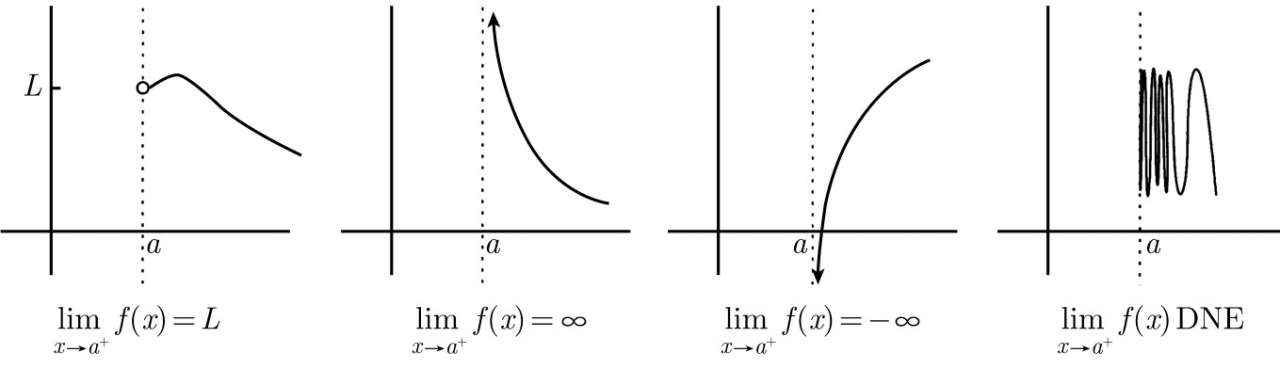
2、在x=a时的左极限，这时在x=a的右侧以及x=a处f(x)的行为是无关紧要的。

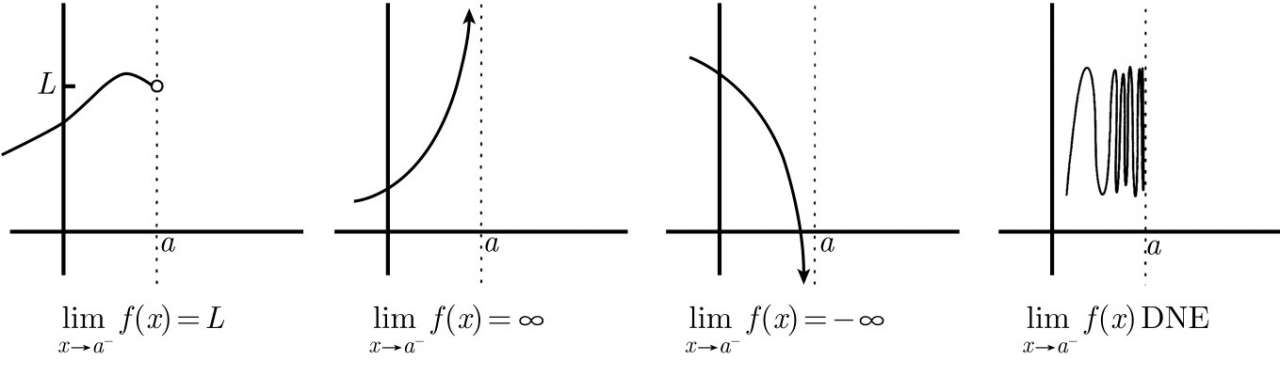
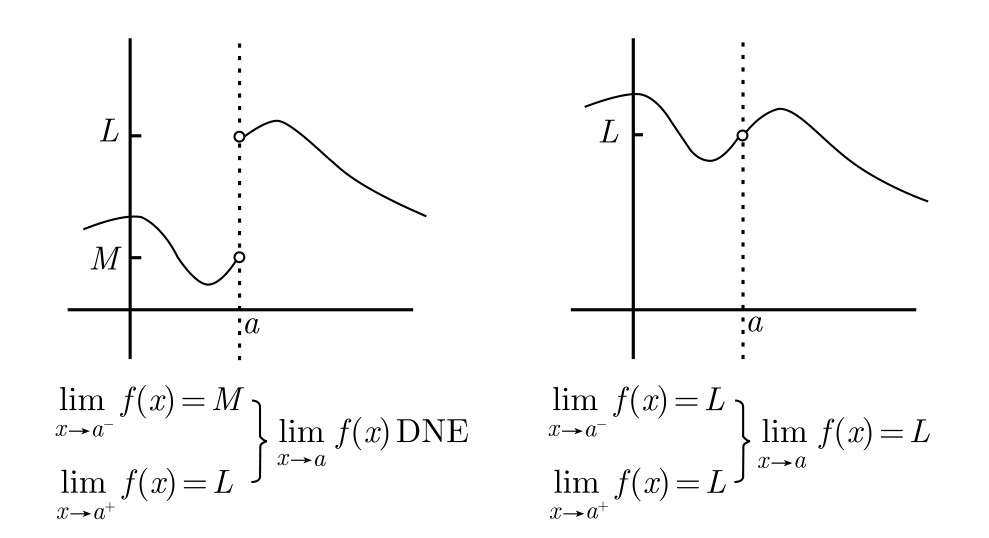
3、在x=a时的双侧极限，在左图中，左极限和右极限存在但不相等，因此，双侧极限不存在。在右图中，左极限和右极限存在并相等，因此，双侧极限存在并等于左右极限值。f(a)的值是无关紧要的。

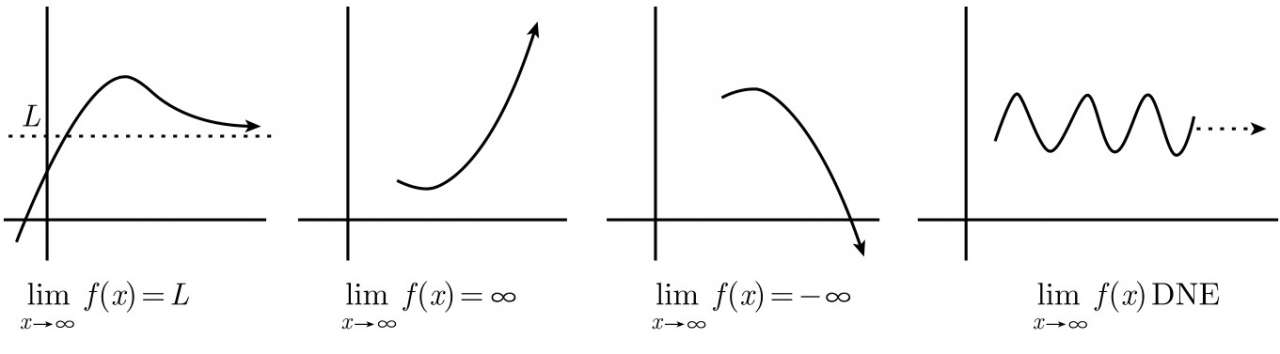
4、在x→∞时的极限

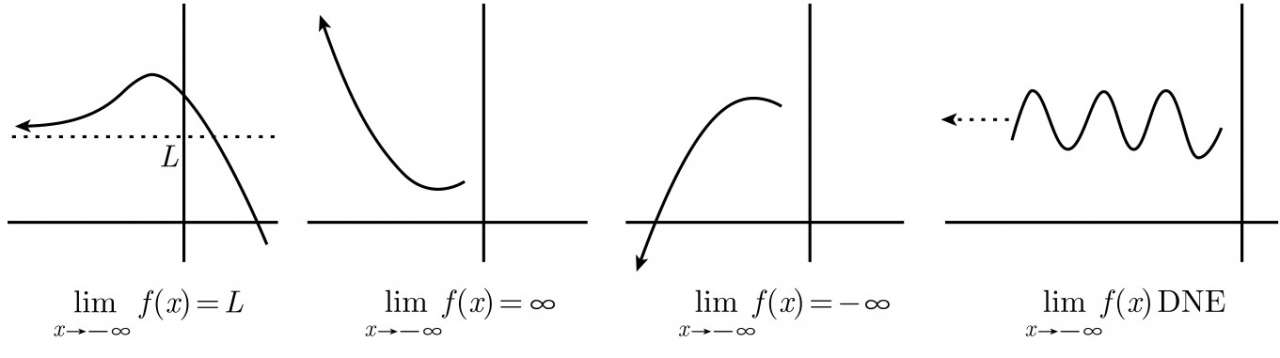
5、在x→-∞时的极限

总结：

极限的四种取值类型

• 定值L
• DNE(震荡)

极限的四种情形：

• 定点左极限
• 定点右极限
• 定点双侧极限

求解趋于常数与无穷的类别

x趋于a时的有理函数极限

1、首先常数用a，替换x，如果式子分母不为0，那么极限值就是替换后得到的值

例如：

2、但是下面这道题我们直接带入2，化简后就得到0了，显然是不对的。这个时候我们可以先进行因式分解

注意

化简为0/0，这被称作不定式，这意味着它什么都可能发生，它的极限或许是有限亦或者是无穷。

要是分母为0，但分子不为0又会怎样呢？这个时候总会有一条存在4种情况的渐近线，只需要分辨f(x)在x=a两边的符号就可以了

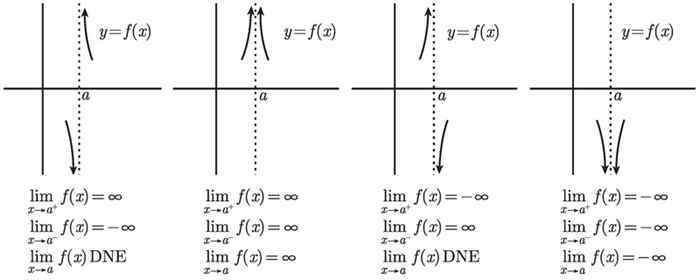
例如两边都是正的，那么就是第二种情况。

例题：

最后发现分母还是为0，我们可以考虑用洛必达来进行求解，这个后续会提到。

这个式子的关键因子是(x-1)，当它比1大一点的时候，为正。当他比1小一点的时候，为负，对比上述图只有第三幅符合条件（从右往左走）。因此我们可以称它为双侧极限不存在，而单侧极限是存在的，于是便得出

此时如果我们做一下微小的调整，将分母的3次方改为2次方呢？我们会得到当x>1时，结果仍然为负数，当x<1时，结果仍然为负数，因为分子始终会为负。因此最终会得到单侧极限为负无穷。

x→a时的平方根的极限

在分母有理化的时候．其基本思想是，a-b的共轭表达式是a+b，反之依然。如果你碰到一个平方根加上或减去另外一个量，可以试着把分子分母同时乘以其共轭表达式。

x→∞时的有理函数的极限

整理后的多项式首项，即x的最大次方项，当x很大时，首项决定一切．这就是说，如果你有一个多项式p，那么当x变得越来越大时，p(x)的表现就好像只有它的首项存在一样。微分也可以理解为变化的速率，一个值加无穷小无穷小存在但是对结果没有影响

和的极限等于极限的和，这在所有的有限极限中成立

当看到某个关于p的多项式p（x）是多于一项时，把它代以

对于每一个多项式都这样做！注意到，所需做的就是用该多项式除以并乘以其首项，因此并没有改变p(x)的量．这里的要点是，当x→∞时，以上表达式中的分式的极限是1，并且首项比原来的表达式简单得多．

这里分母的次数为2，大于分子的次1．结果是，分母占主导，因此极限为0

小结

其中p和q为多项式，我们可以说：

（1）如果p的次数等于q的次数，则极限是有限的且非零；

（2）如果p的次数大于q的次数，则极限是∞或-∞；

（3）如果p的次数小于q的次数，则极限是0.

x→∞时的多项式型函数的极限

这道题如果我们直接将分子带入，最后求得结果会是，这属于不定式，在这道题中，显然是不对的。因此我们可以考虑用共轭式子来进行求解

x→∞与x→-∞的差异

对于某个正的n，当x→-∞时，任何形如C/xn的项都会趋于0，与当x→∞时的情形是一样的。具体的差异如下：

趋向正无穷和趋向负无穷在求解极限时可能会有一些差异，具体体现在以下几个方面：

1. 奇偶性

• 如果函数是偶函数（例如），那么当时，函数的极限是相同的。
• 如果函数是奇函数（例如 ），那么在趋向正无穷和负无穷时，函数的极限可能不同。

2. 符号变化

• 对于包含奇次幂的函数（例如或x），当x趋向负无穷时，函数的符号会发生变化。例如，。
• 对于偶次幂的函数（例如 或），无论 xx 趋向正无穷还是负无穷，函数的值都将是正的。

3. 绝对值的影响

• 对于带有绝对值的函数，趋向正无穷和负无穷的极限可能会不同。例如：, 但对于像这样的函数，趋向负无穷时函数值的符号变化可能会影响其极限的计算。

4. 复合函数的行为

• 如果是复合函数，尤其是带有对数、指数等运算的函数，可能在正负无穷情况下行为不同。例如：
  • 对于，只有当时极限存在，时则没有定义。
  • 对于指数函数，当 时，，而当时，。

5. 分式的行为

• 在求分式的极限时，分子和分母的符号及其增长速度（尤其是在含有 xx 的分数形式时）也可能导致正无穷和负无穷的极限结果不同。例如：

6. 根号的行为

• 如果是涉及根号的表达式，比如 ，那么趋向正无穷和负无穷时可能会有不同的结果。例如： .

这取决于根号下的数值和x的符号。

总结：

• 正无穷和负无穷的主要差异在于符号的变化，特别是在奇次幂、分式、复合函数等情况下。
• 需要根据具体的函数来分析它在正无穷和负无穷处的行为，可能会有完全不同的极限值，尤其是在涉及到符号变化、绝对值、分母的情况下。

x→-∞时的有理函数的极限

例题1：

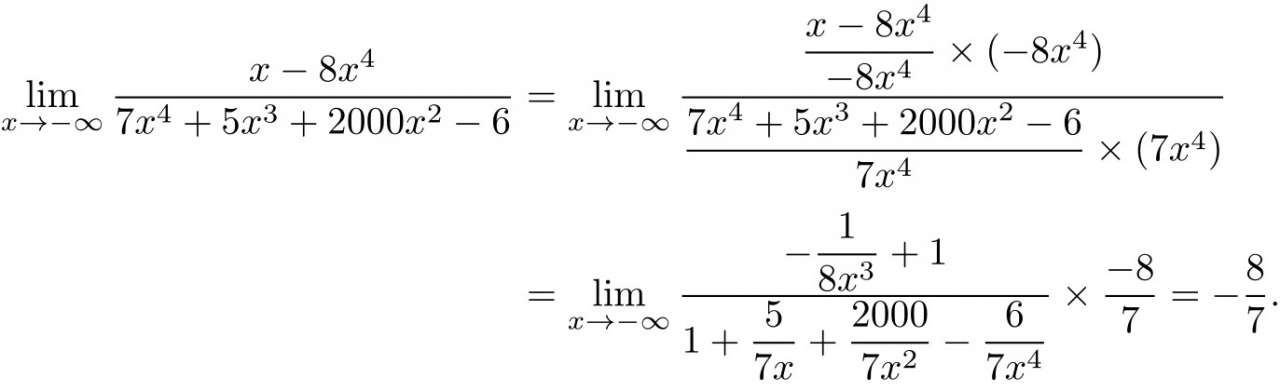
例题2：

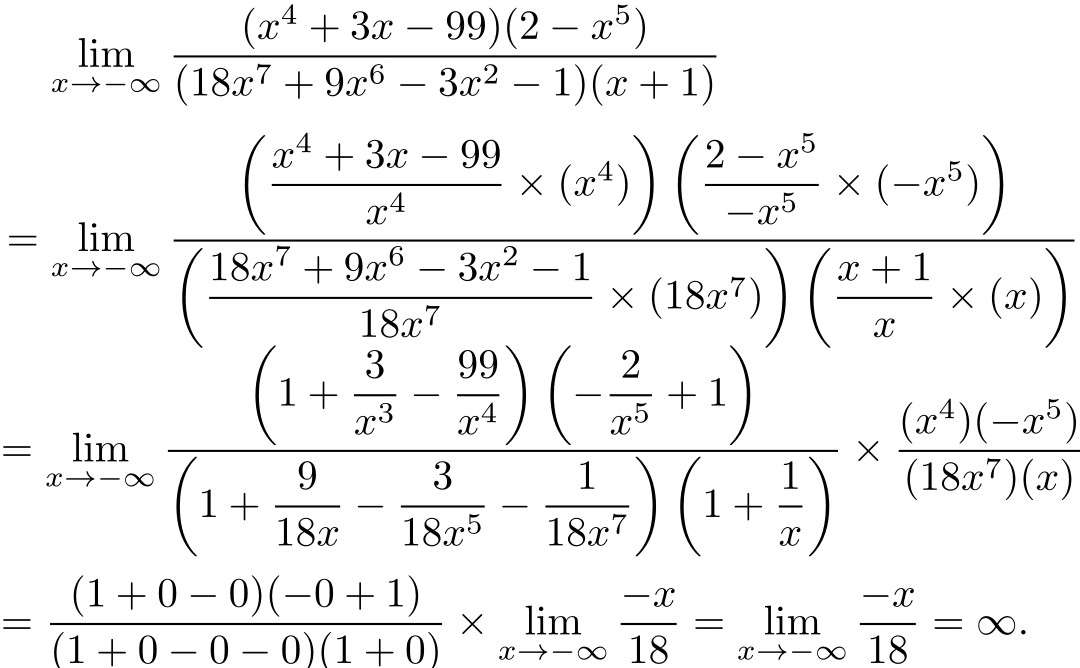
例题3：

此题注意：，根据根式的性质，任何数n次方开n次方根，n为奇数等于本身，为偶数等于绝对值，因此得注意变号

• 偶次幂（如 等）在负无穷时的符号和正无穷时相同。
• 奇次幂（如 等）在负无穷时的符号和正无穷时相反。
• 对于一个分式，最终符号由分子和分母的最高次项的符号决定。

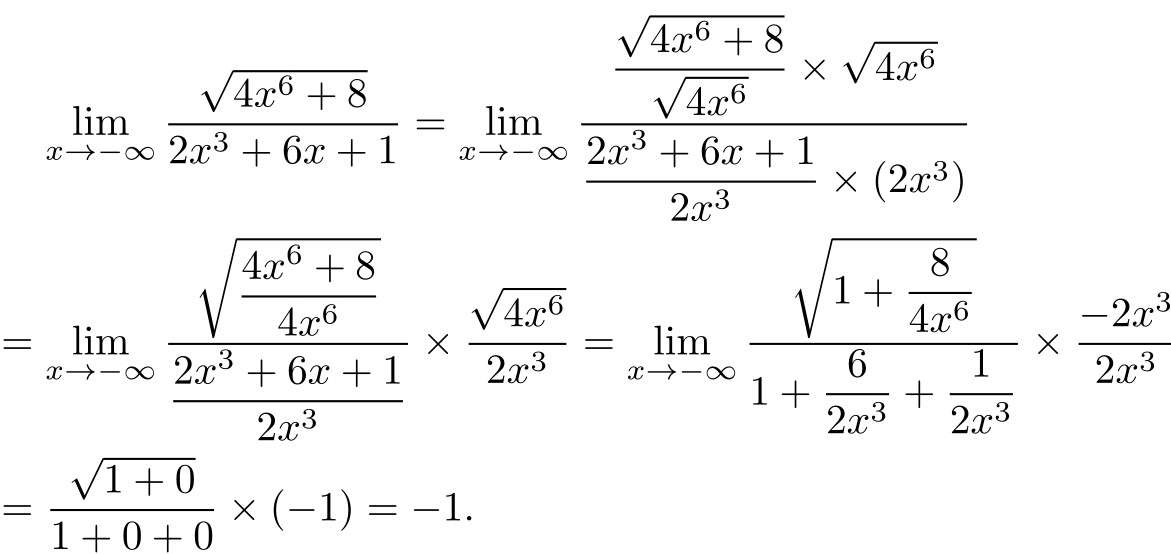
包含绝对值的函数的极限

看一看这个绝对值，就会发现，它取决于x+2≥0还是x+2<0．这些条件可以被重新写成x≥-2或x<-2。

在第一种情况下，|x+2|=x+2；

而在第二种情况下，|x+2|=-(x+2)

最后的结果是，当x>-2时，|x+2|/(x+2)等于1；

而当x<-2时，它则是-1。事实上，y=|x+2|/(x+2)的图像就是y=|x|/x的图像向左平移两个单位得到的，如

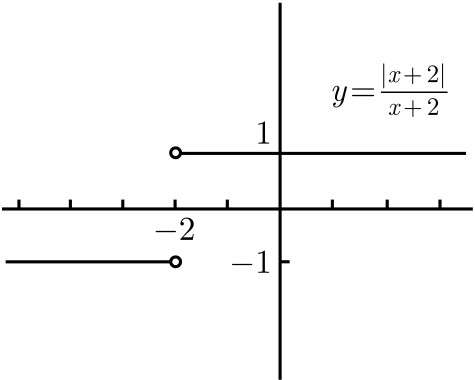
这就是说，要求的左极限等于-1（同时，右极限是1，故双侧极限不存在

参考资料

普林斯顿微积分读本