微积分03:导数

1. 引言

   本章重点

   • 连续性
   • 可导性
   • 二阶导数与高阶导数

   连续的定义

   点上连续

   1. 双侧极限存在，并且是有极限的：
   2. 函数在点x=a处有定义，即f(a)存在并且是有限的
   3. 以上两个量相等，即

   不满足会有什么情况？

   

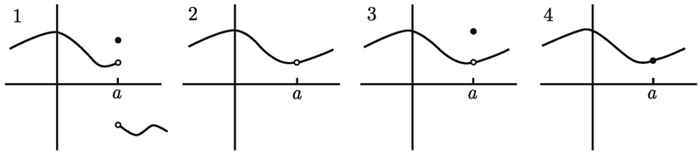
   • 图1是左极限右极限不相等，所以双侧极限不存在。因此函数在x=a处，不连续
   • 图2左右极限都存在且相等，故而双侧极限存在，然而函数在点x=a处无定义，因此函数在x=a处不连续
   • 图3双侧极限存在，函数在x=a时有定义，但极限值和函数值不相等，因此函数在店x=a处一次不连续。
   • 图4双侧极限存在，f(a)存在，并且极限值和函数值相等，因此确定函数x=a处连续

未完待续….