二叉树

二叉树的基本概念

若一个高度为k的二叉树有2^k -1个结点，那么就称该二叉树为满二叉树。由连续编号任意多个结点组成的二叉树称为完全二叉树。

二叉树的层级性质

在二叉树的第i层上至多有2^(i-1)个结点（求的是某一层节点的数量）

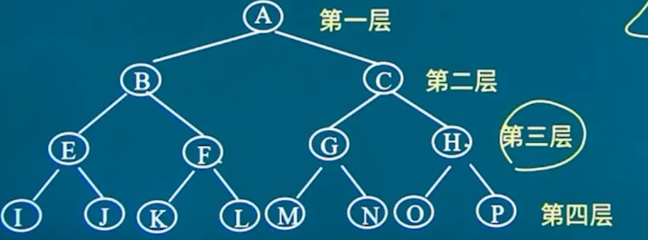
二叉树的深度性质

深度为k的二叉树，至多有2^k -1个结点（求的是某一个节点的总数）

二叉树叶子结点性质

对于任意二叉树，如果终端节点为n0，度为2的结点数为n2。则n0=n2+1，即叶子结点数 n0= 度为2的结点数n2+1。

代码实现

结构体定义

#include <iostream>
using namespace std;
typedef struct btnode {
    int data;
    struct btnode* lchild, * rchild;
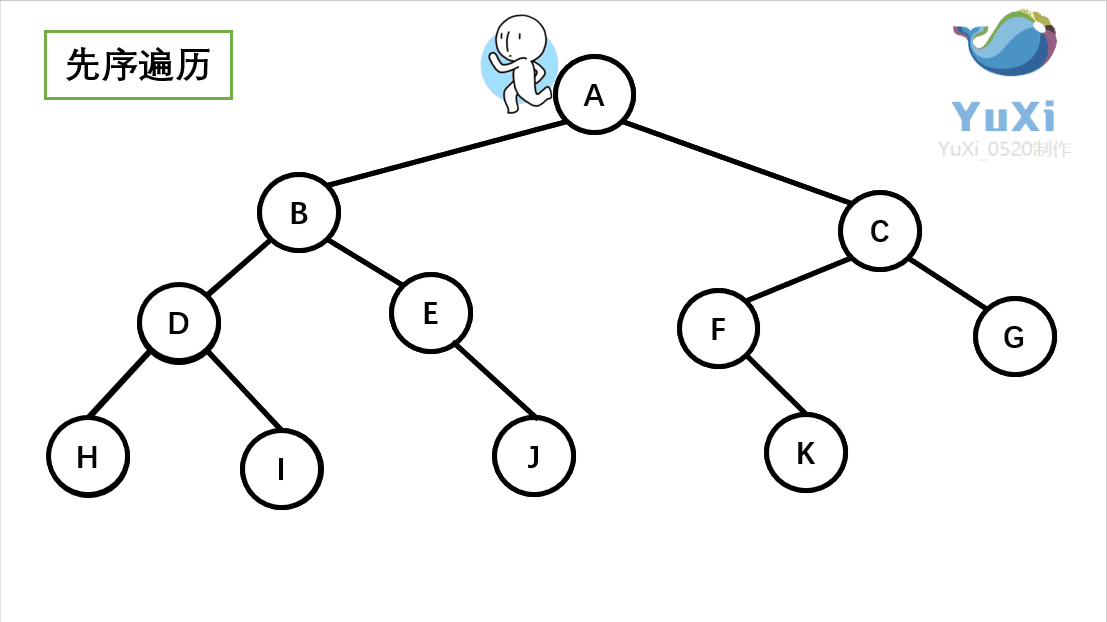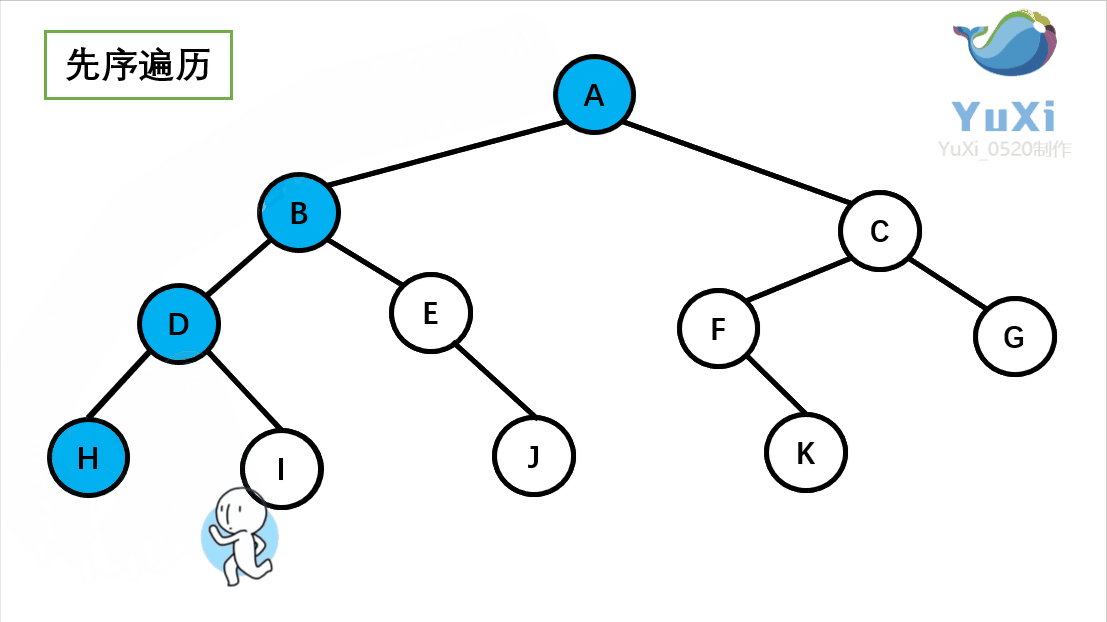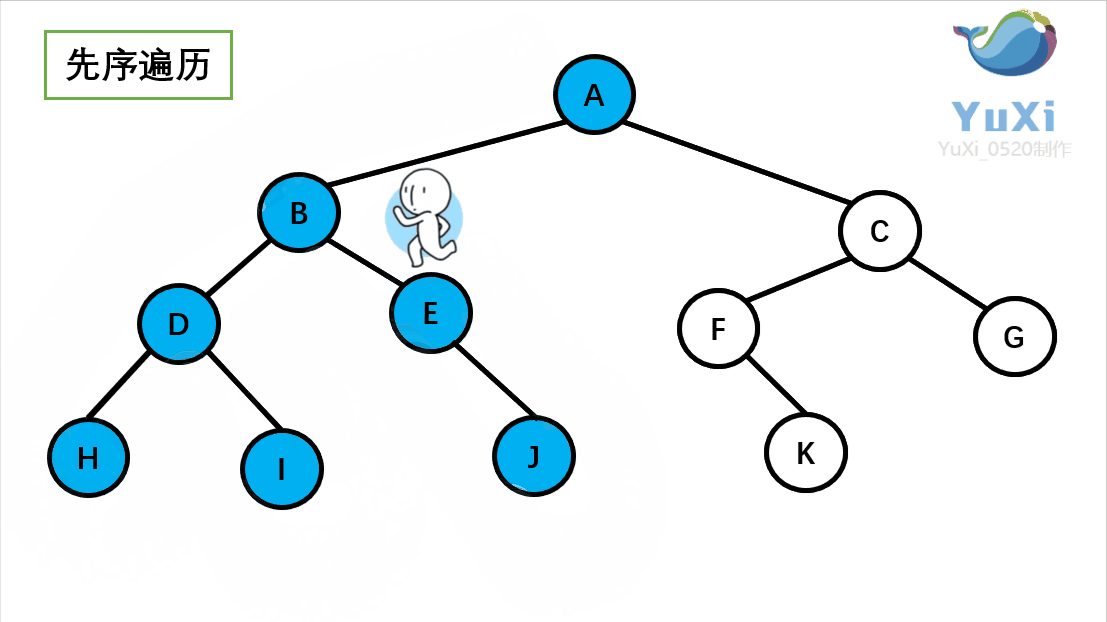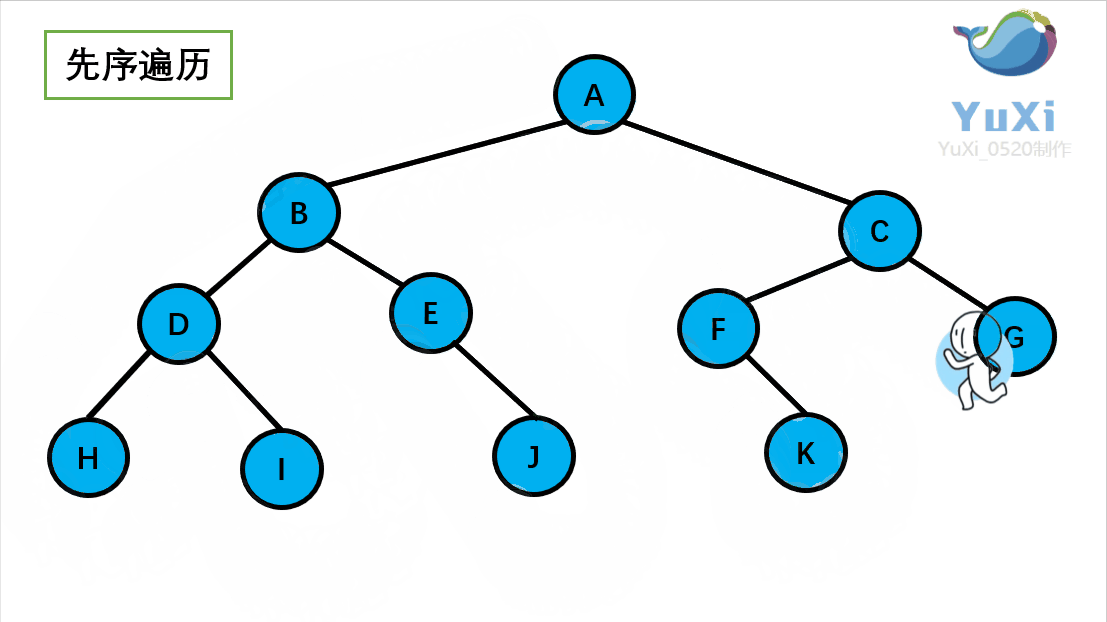
}*BinTree;

先序遍历：根节点，左子树，右子树

//先序遍历
void preorder(BinTree bt) {
    if (bt != NULL) {
        cout << bt->data << endl;
        preorder(bt->lchild);
        preorder(bt->rchild);
    }
}

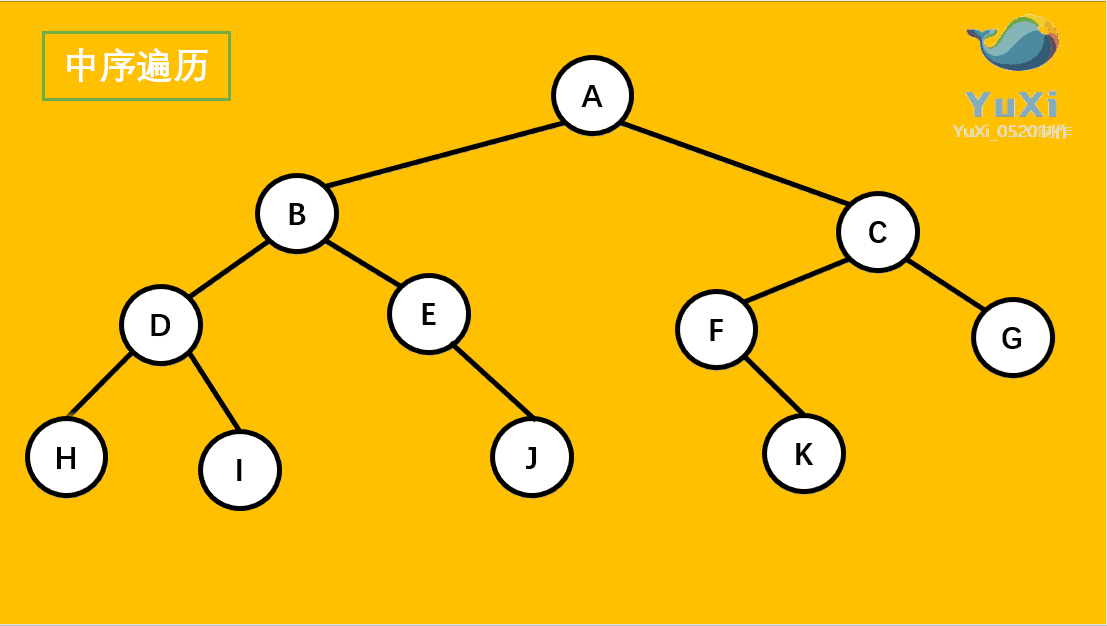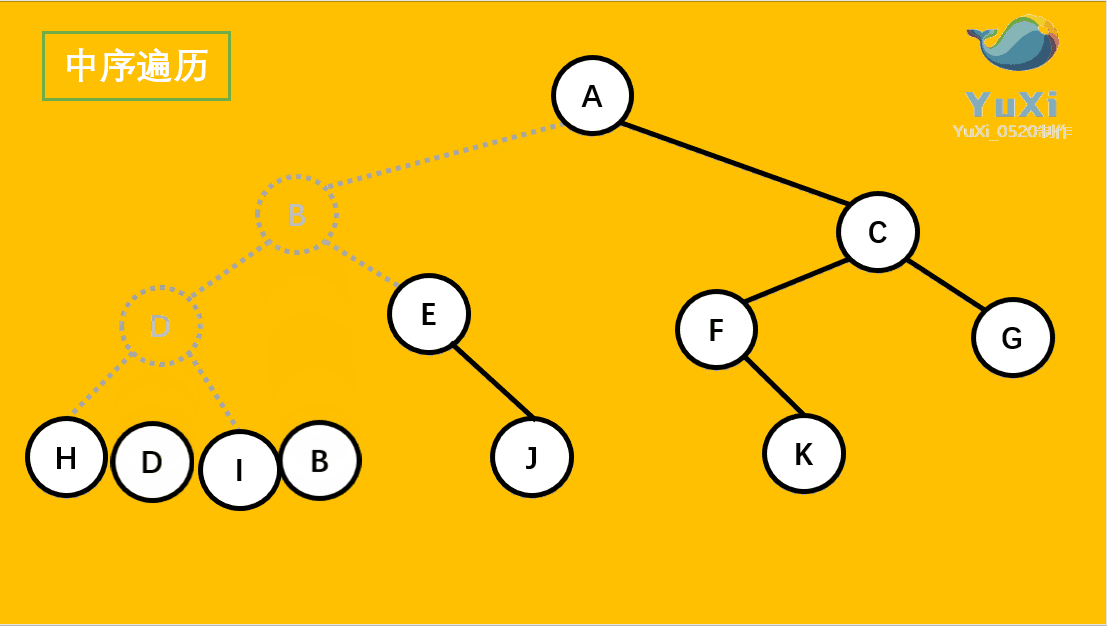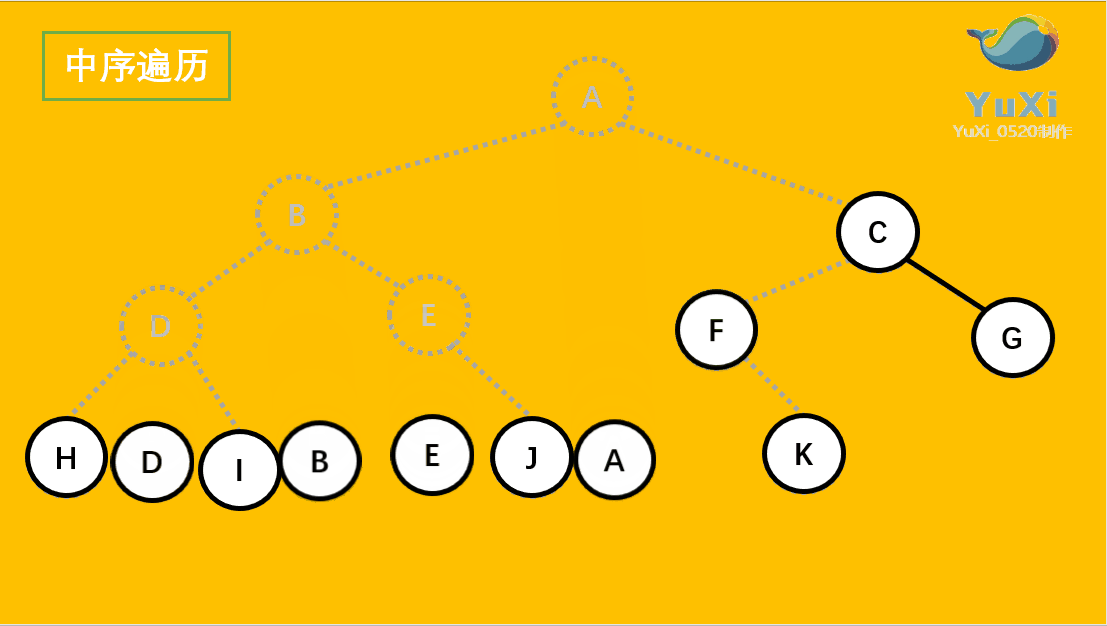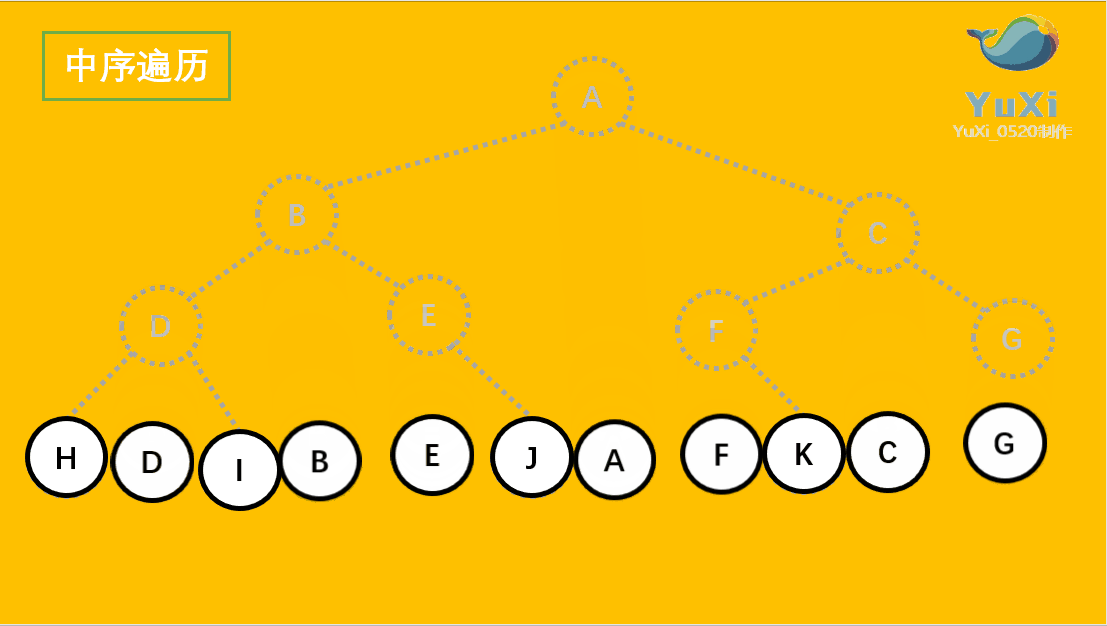
中序遍历：左子树，根节点，右子树

//中序遍历
void Inorder(BinTree bt) {
    if (bt!=NULL) {
        Inorder(bt->lchild);
        cout << bt->data << endl;
        Inorder(bt->rchild);
    }
}

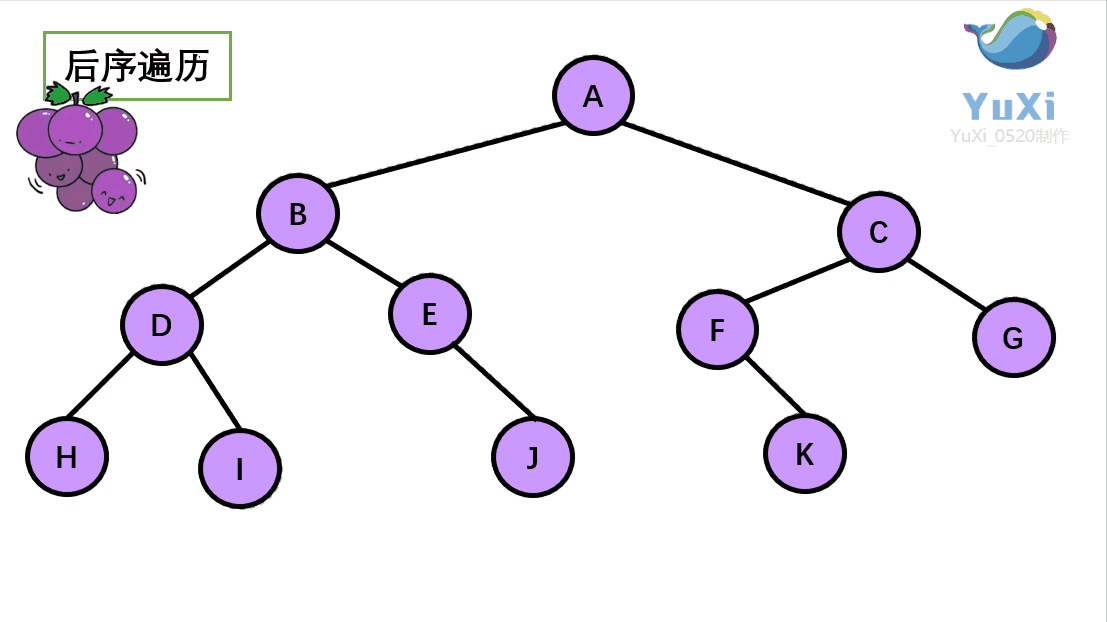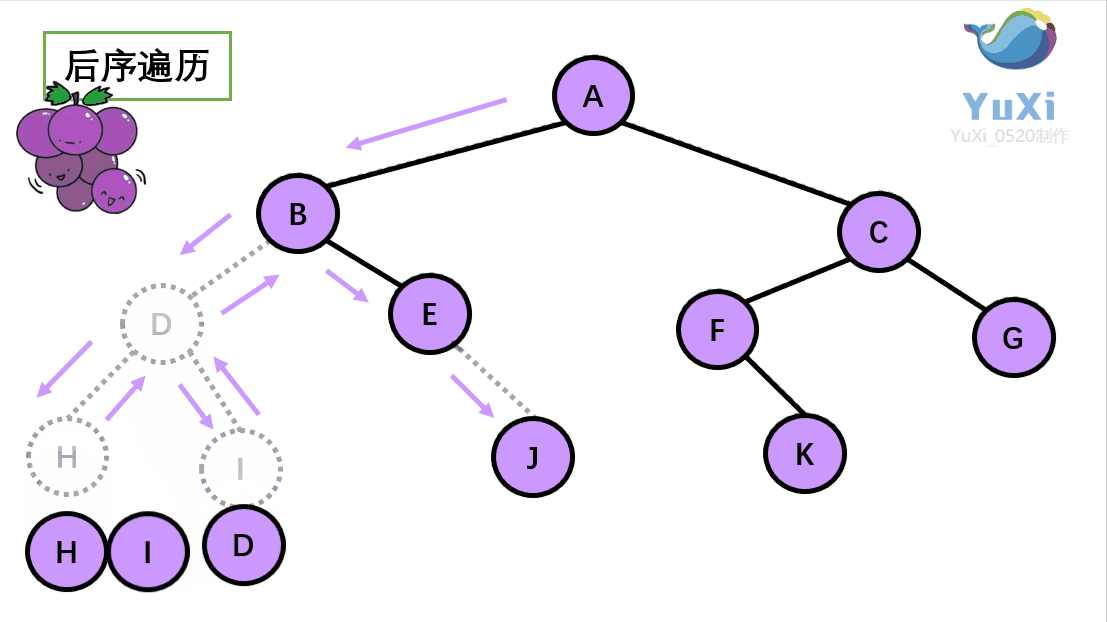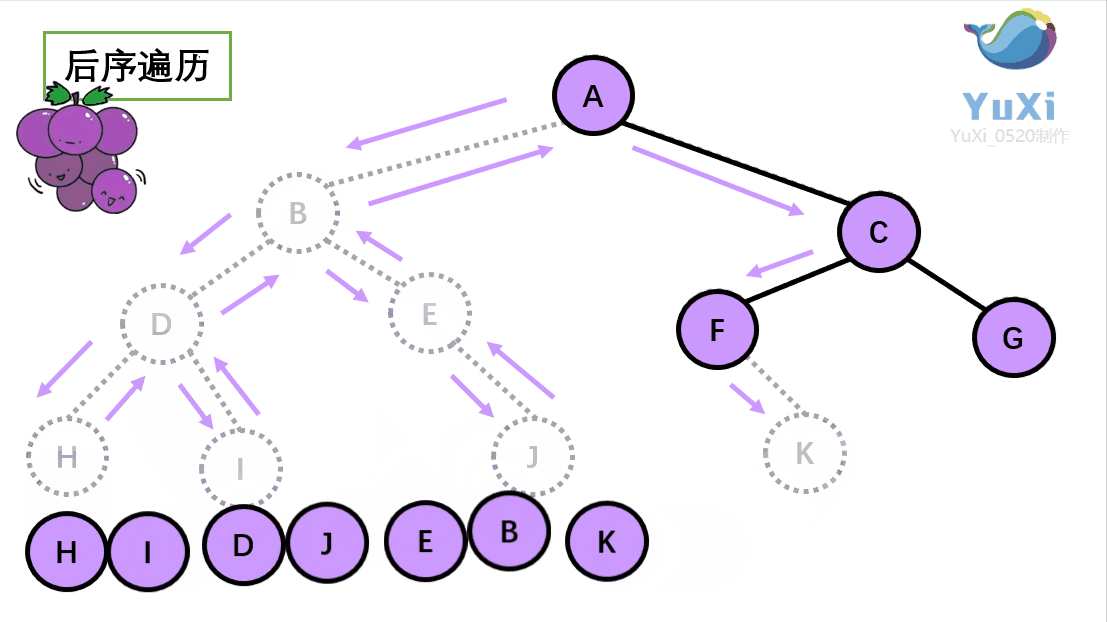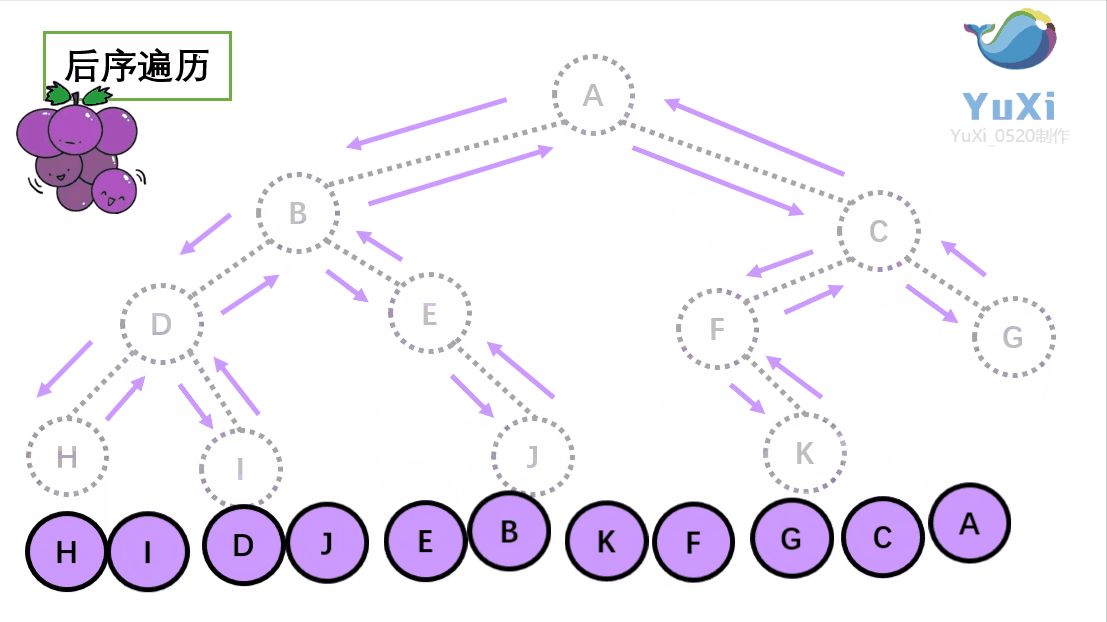
后续遍历：左子树、右子树、根节点

//后续遍历
void Postorder(BinTree bt) {
    if (bt!=NULL) {
        Postorder(bt->lchild);
        Postorder(bt->rchild);
        cout<< bt->data << endl;
    }
}