树与森林

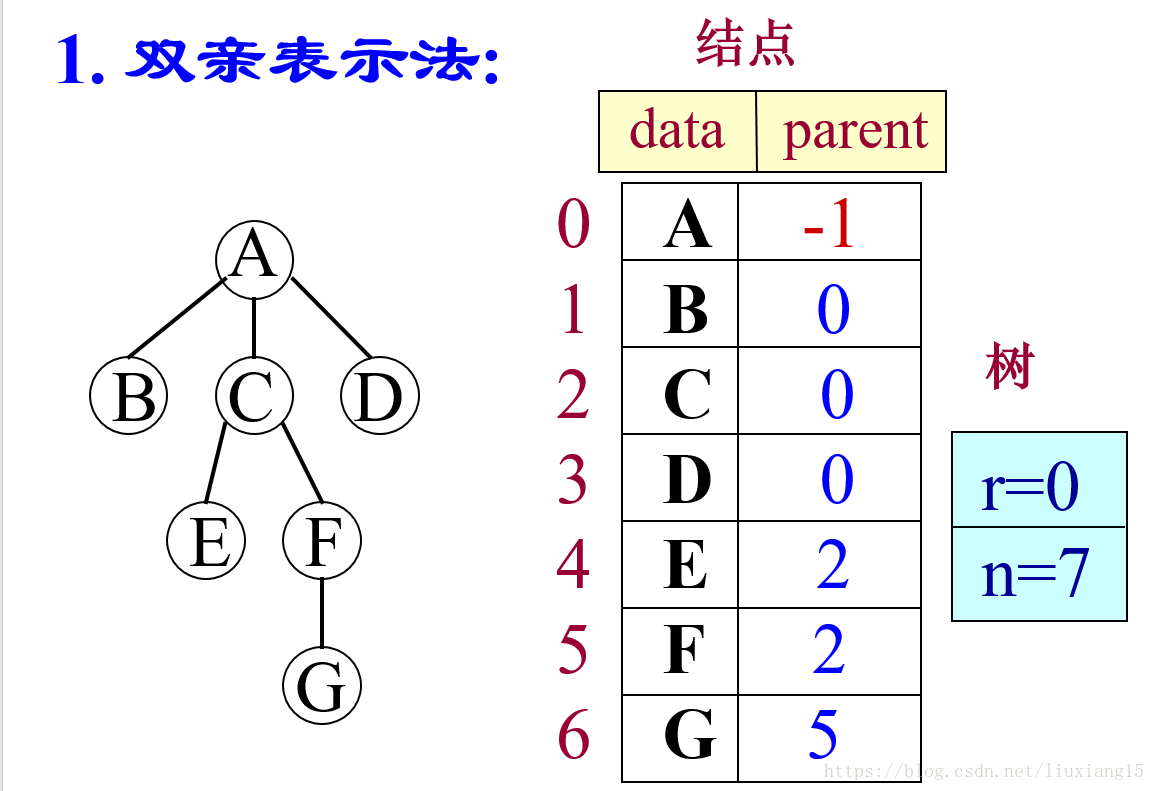
双亲表示法

定义一个数组，数组中存放输的节点，每个节点包含数据域与双亲域。

双亲域表示当前节点的双亲的在数组中的下标

typedef struct PTNode{
    ElemType data;
    int parent;
}PTNode;

typedef struct PTree
{
    PTNode nodes[MAXQSIZE];
    int r,n //根节点的位置和总元素个数
};

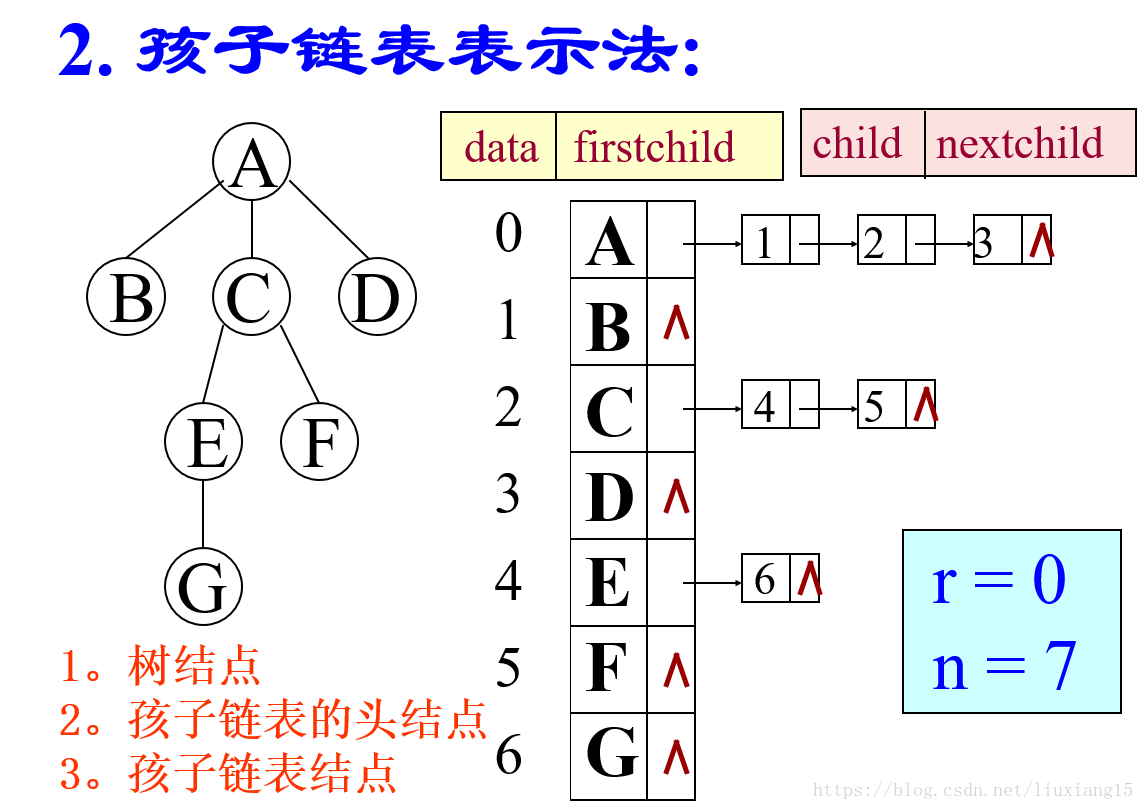
孩子链表示法

把每个节点用线性表连接起来，把某个节点的所有孩子节点连接成为一个单链表，连接在其父节点的线性表中

typedef struct CTNode
{
    int child;
    struct CTNode next;
}ChildPtr; //孩子节点

typedef struct{
    ElemType data;
    ChildPtr firstchild;
}CTbox; //双亲节点

typedef struct{
    CTbox nodes[MAXQSIZE];
    int n,r;//根节点数与根节点的位置
}CTree;

孩子兄弟表示法（二叉树表示法、二叉链表表示法）

用二叉链表作为树的存储结构，链表中每个节点的两个指针域分别指向其第一个孩子节点和下一个兄弟节点

typedef struct CSNode{
    ElemType data;
    struct CSNode firstchild,nextsibling;
}CSNode,CSTree;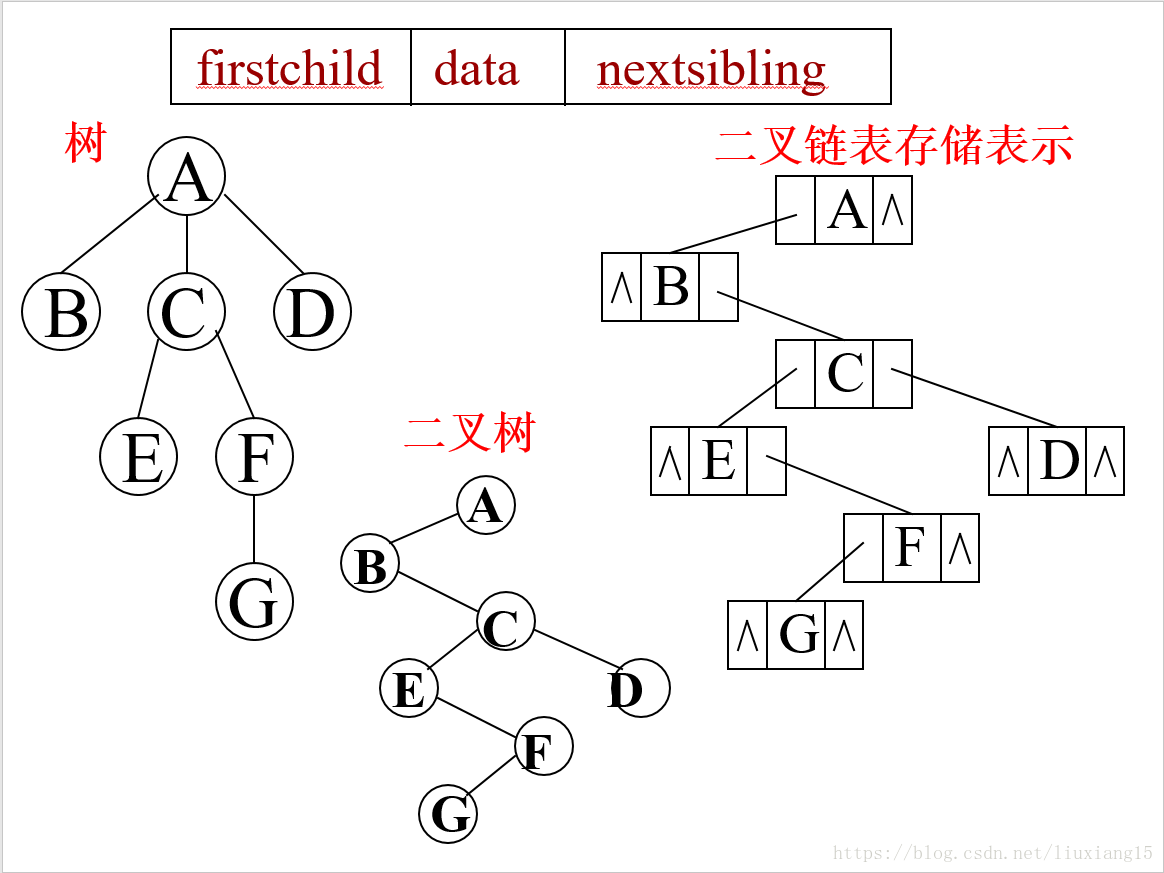

树转二叉树

树转为二叉树转换步骤如下

1. 加线：兄弟之间加一条线
2. 抹线：对每个节点，除了其左孩子之外，去除与其他孩子之间的关系
3. 旋转：以树的根节点为轴心，整棵树顺时针旋转 40°

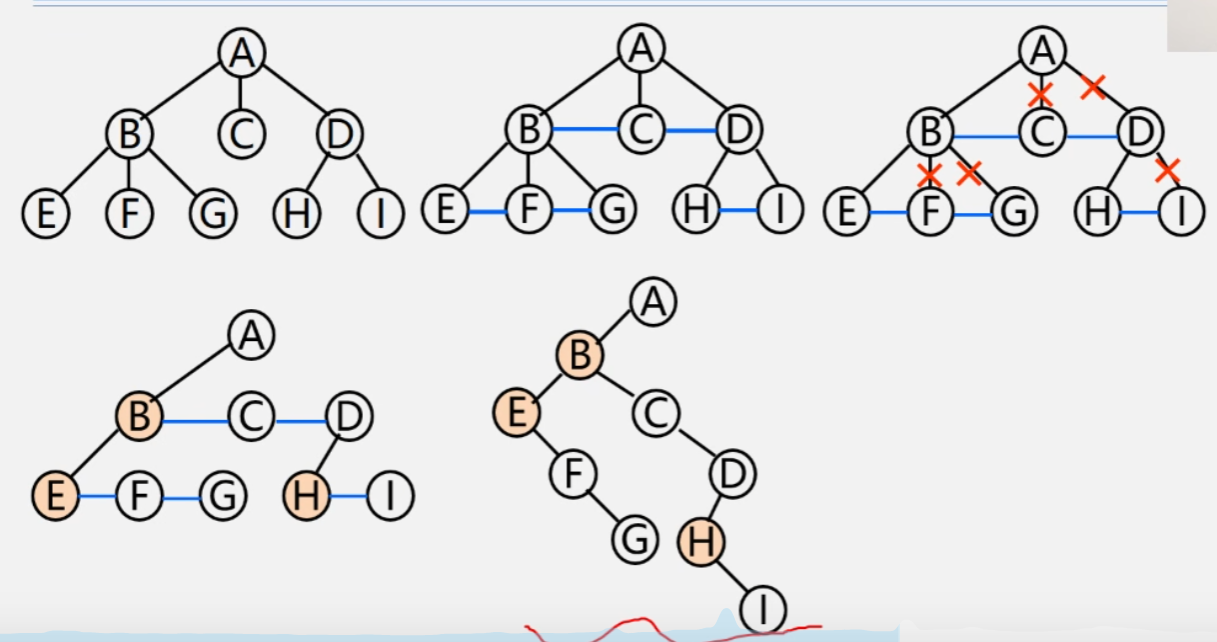
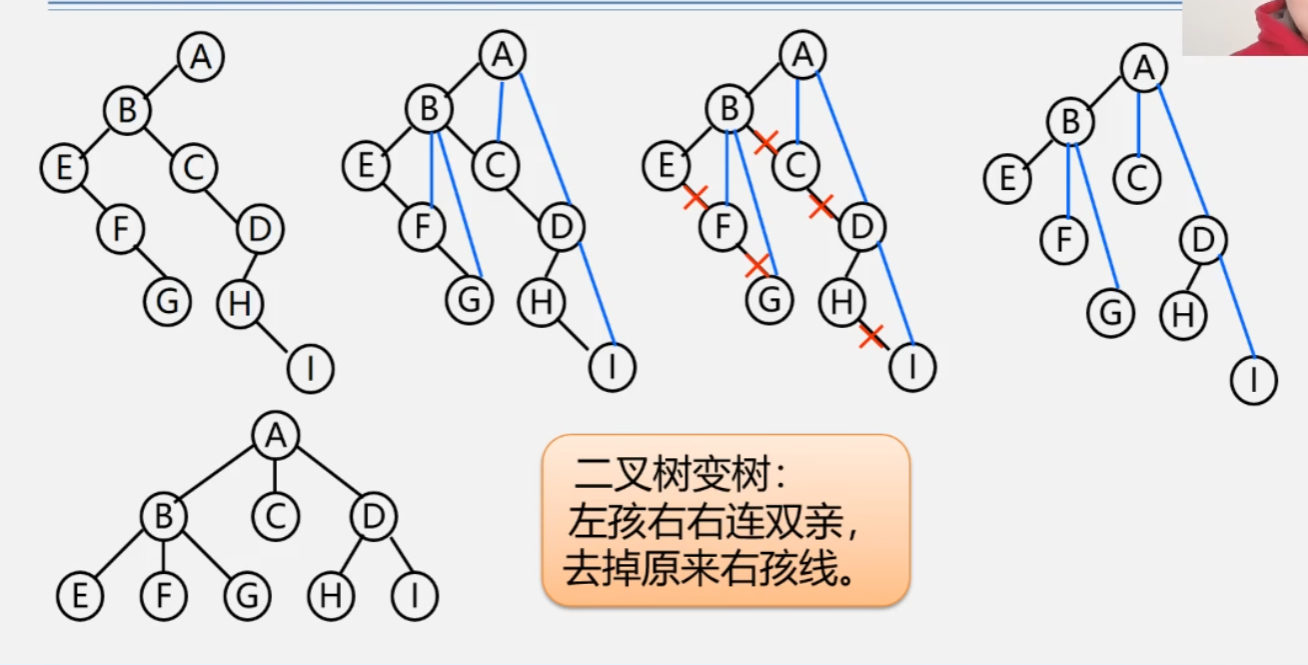
二叉树转树

1. 加线：若 p 节点是双亲节点的左孩子，则将 p 的右孩子、右孩子的右孩子……. 沿着分支找到的所有右孩子，都与 p 的双亲用线连接起来
2. 抹线：抹掉原来二叉树的双亲节点与右孩子之间的连线
3. 调整：将节点按层次排列一下

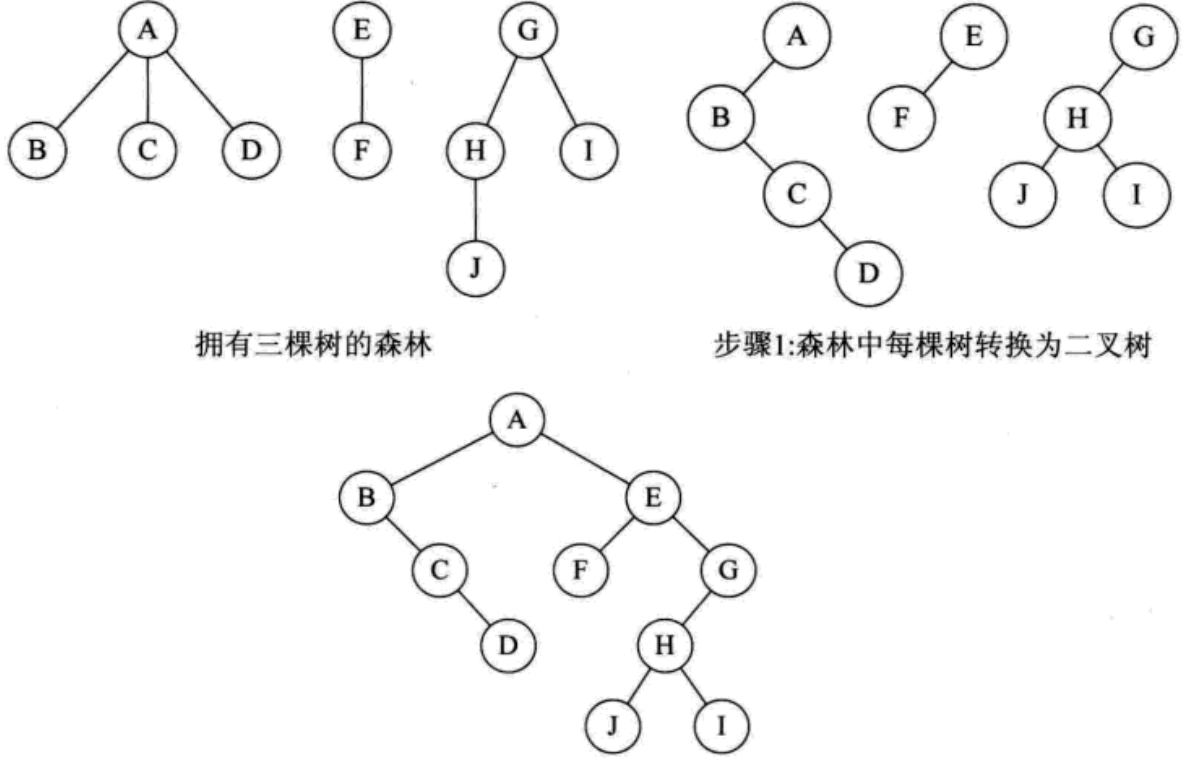
森林转二叉树

转换：将森林中的每一颗树转换成二叉树;

连线：将各颗转换后的二叉树的根结点相连；

旋转：将添加的水平线和原有的连线,以第一颗树的根结点为轴心,按顺时针方向旋转45°

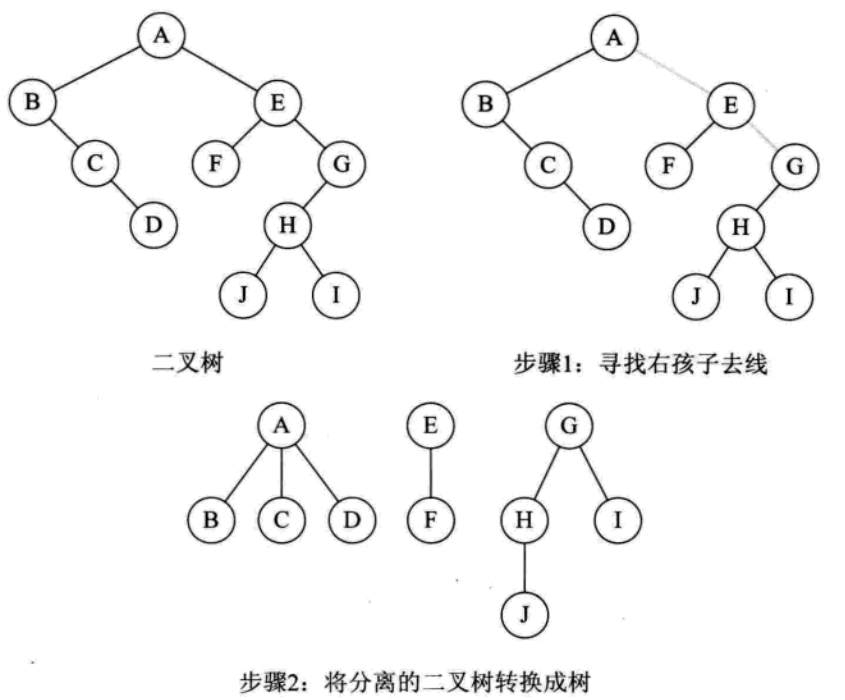
二叉树转森林

1. 从根结点开始，若右孩子存在，则把右孩子结点的连线删除，在查看分离后的二叉树，若右孩子存在，则连线删除……，直到所有的右孩子连线都删除为止，得到分离后的二叉树。
2. 在将每棵分离后的二叉树转换为树即可。

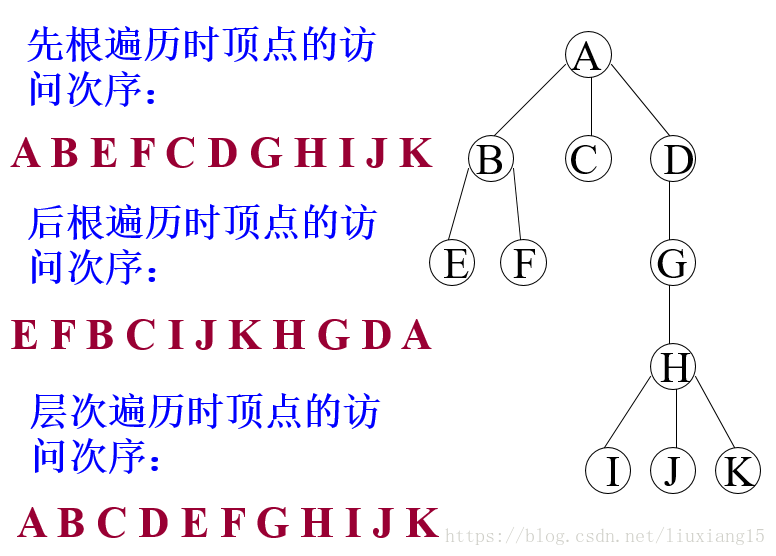
树的遍历有三种搜索策略

先根遍历:若树不空，则先访问根结点，然后依次先根遍历各棵子树。

后根遍历:若树不空，则先依次后根遍历各棵子树，然后访问根结点。

按层次遍历:若树不空，则自上而下自左至右访问树中每个结点。（用队列+递归实现）

森林的遍历

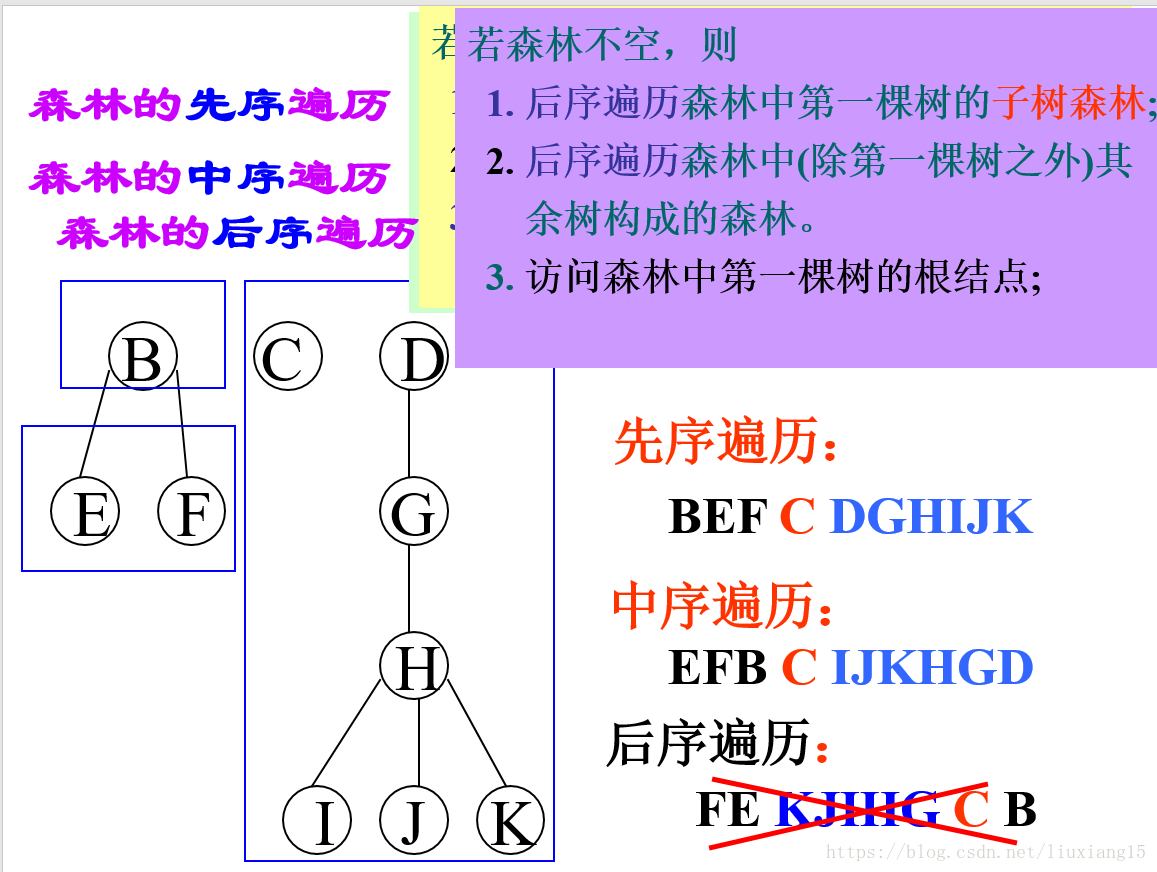
• 森林的先序遍历：若森林不空，则

• 访问森林中第一棵树的根结点

• 先序遍历森林中第一棵树的子树森林;

• 先序遍历森林中(除第一棵树之外)其余树构成的森林。

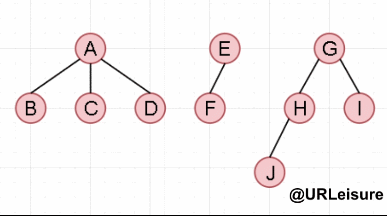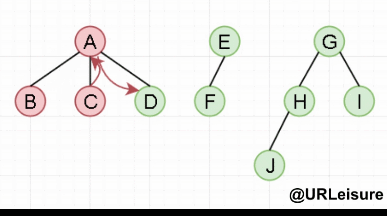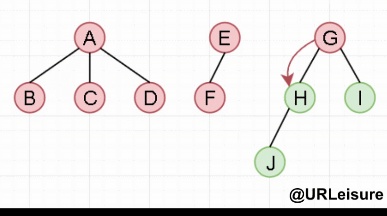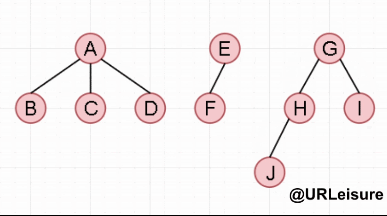
先序遍历：ABCDEFGHJI

• 森林的中序遍历：若森林不空，则

  • 中序遍历森林中第一棵树的子树森林;

  • 访问森林中第一棵树的根结点;

  • 中序遍历森林中(除第一棵树之外)其余树构成的森林。

    

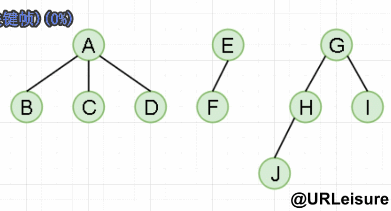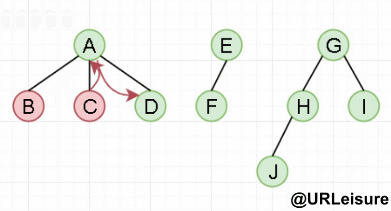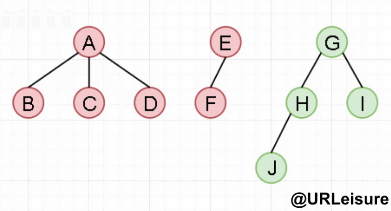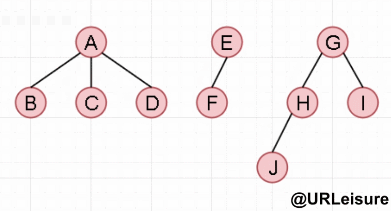
    中序遍历：BCDAFEJHIG