定义
索洛增长模型的设计是为了说明在一个经济中,资本存量的增长、劳动力的增长和技术进步如何相互作用,以及它们如何影响一国产品与服务的总产出。
建模——产品的供给与生产函数
产品的供给与生产函数 索洛模型中产品的供给是基于生产函数的。生产函数是说,产出取决于资本存量和劳动力:
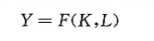
索洛模型假设生产函数具有不变规模报酬,那么,生产函数就具有不变规模报酬。也就是说,如果资本和劳动变为原来的z倍,那么,产出量也变为原来的z倍。
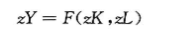
规模报酬不变的生产函数使我们可以分析经济中所有数量相对于劳动力规模的值。为了看出这一点,设在前面的方程中x=1/L,得到
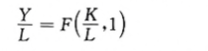
这个方程表示,人均产出Y/L是人均资本量K/L的函数。(数字“1”是常数,从而可以忽略。)规模报酬不变的假设意味着,经济的规模——用工人人数来衡量——不影响人均产出和人均资本量之间的关系。
由于经济规模是无关紧要的,所以,可以用人均值来表示所有数量。我们用小写字母表示人均量,因此,y=Y/L是人均产出,k=K/L是人均资本量。这样,我们可以把生产函数写为:y=f(k)
式中,我们定义f(k)=F(k,1),于是我们得到一副这样的图
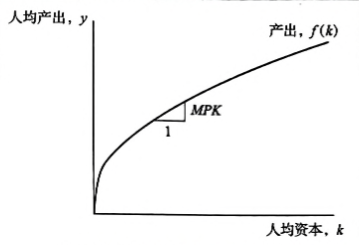
生产函数表示人均资本量k如何决定人均产出量y=f(k)。生产丽数的斜率是资本的边际产量:如果k增加1单位,y增加MPK单位。随着k的增加,生产函数变得越来越平坦,这表明资本的边际产量递减。
这一生产函数的斜率表示当给一个工人一单位额外资本时,他生产的额外产出是多少。这个量是资本的边际产量(MPK)。在数学上,我们写为
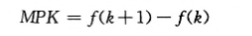
建模——产品的需求与消费函数
在索洛模型中,产品的需求来自消费和投资,人均产出y,被划分为人均消费c和人均投资i:y=c十i
注意该方程假设是一个封闭经济,忽略了政府购买和净出口
索洛模型假设每年人们储蓄s比例的收人,消费(1-s)比例的收人:c=(1-s)y
为了看出这一消费函数对投资意味着什么,用(1-s)y代替国民收入核算恒等式中的c:
y=(1-s)y+i
整理后得到:i=sy,这个方程表明,投资等于储蓄。因此储蓄率s也是用于投资的产出比例。
小结
现在完成了索洛模型中的两个主要组成部分——生产函数和消费函数,它们描述了任何一个时点上的经济。对于任何一个给定的资本存量k,生产函数y=f(k)决定了经济生产多少产出,储蓄率s决定了产出在消费和投资之间的配置。
资本存量的增长与稳定状态
人均投资i等于sy。通过用生产函数替代,我们可以把人均投资表示为人均资本存量的函数:i= sf(k)。这个方程把现有资本存量k与新资本的积累i联系在一起,就有了下图:
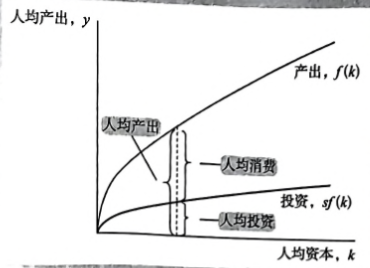
储蓄率s决定了产出在消费和投资之间的配置。对于任意资本水平k,产出是f(k),投资是sf(k),消费是f(k)一sf(k)。
该图说明了,对任何一个k值,产出量如何由生产函数f(k)决定以及那些产出在消费和储蓄之间的配置如何由储蓄率s决定。
我们用δ表示折旧,每年折旧的资本量是δk,于是就会有下图:
资本和折旧对资本存量的影响表示为如下方程:
资本存量的变动=投资 - 折旧 =>:Δk = i - δk,
Δk为某年和下一年之间资本存量的变动,由于投资i等于sf(k),我们可以把方程写为:Δk = sf(k) - δk
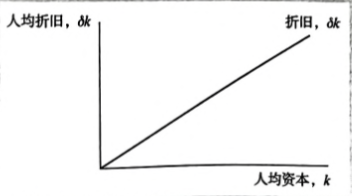
此图说明了折旧量是如何取决于资本存量
每年有不变比例δ的资本存盘被磨损。因此,折旧与资本存量是成比例的。
存在单一的资本存量k使得投资量等于折旧量。如果经济发现自身正处于这一资本存量水平,那么,资本存量就不会改变,因为作用于它的两种力量:投资和折旧,正好平衡了。也就是说,在k点,Δk=0,因此,资本存量k和产出f(k)随时间的推移是稳定的(既不增加也不减少)。因此,我们把k称为稳定状态(简称“稳态”)资本水平。
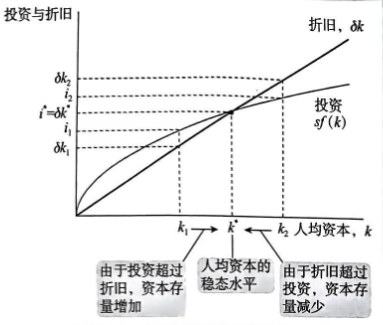
稳态资本水平k是投资等于折旧的水平,表示资本量不随时间而变化。低于k,投资大于折旧,因此资本存量增加;高于k,投资小于折旧,因此资本存量减少。
趋近稳态
假设生产函数为:
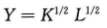
资本份额参数a等于1/2的柯布——道格拉斯生产函数,为了得到人均生产函数f(k),把生产函数两边同时除以劳动力L
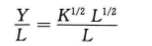
整理后可得:
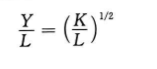
由于y=Y/L和k=K/L,那么这个方程就变成了:
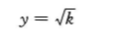
这个形式的生产函数是说,人均产出等于人均资本量的平方根
假设产出的30%用于储蓄(s=0.3),每年有10%的资本存量折旧(8=0.1),经济的初始人均资本为4单位(k=4)。给定这些数字,我们现在可以考察经济随着时间的推移会发生什么变动。
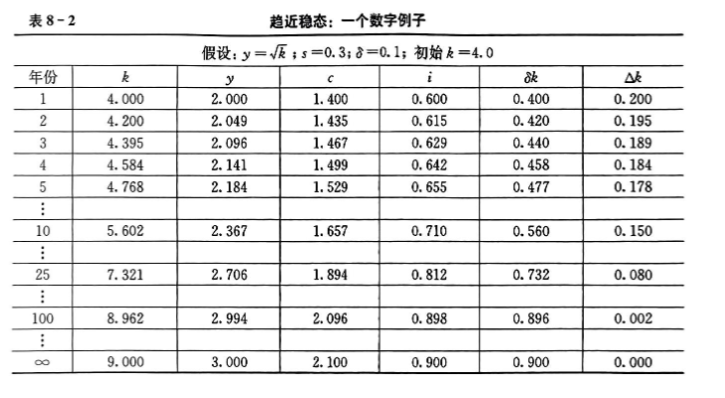
我们对随后的每一年可以做同样的计算。表8-2显示了经济是如何发展的。每一年,由于投资超过折旧,所以,资本存量增加,产出增长。许多年后,经济达到人均资本为9单位的稳态。在这一稳态,0.9单位的投资正好抵消了0.9单位的折旧,因此,资本存量和产出不再增长。
跟踪经济许多年的发展过程是找出稳态资本存量的一种方法,但还有另一种只要求更少量的计算方法:Δk = sf(k) - δk
由于稳态是使得Δk = 0的k值,所以可以推导出:
0 = sf(k) - δk 等价于:
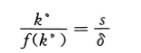
将数字代入生产函数,可得:k=9,由此可知稳态人均资本的存量是9个单位,这也温和8-2表中的稳态计算。
小结
索洛模型表明,储蓄率是稳态资本存量的关键决定因素。如果储蓄率高,经济的稳态将会有大的资本存量和高的产出水平。如果储蓄率低,经济的稳态将会有小的资本存量和低的产出水平。更高的储蓄导致更快的增长,但只是暂时性的。储蓄率的提高加快了增长,但只是在经济达到新的稳态之前。如果经济保持高储蓄率,它会保持大的资本存量和高的产出水平,但它不会永远保持高经济增长率。改变人均收入的稳态增长率的政策被说成是有增长效应。
比较稳态
政策制定者的目的是使组成社会的个体的福利最大化。个体本身并不关心经济中的资本量,甚至也不关心产出量。他们关心的是他们可以消费的产品与服务的数量。因此,一个优秀的政策制定者要选择消费水平最高的稳态。使消费最大化的稳态k值被称为资本的黄金律水平
我们假设稳态的人均产出是f(k*),其中k * 是稳态的人均资本存量,且稳态资本存量不变,所以投资等于折旧δk*,用f(k *)代替y,并用δk *代替i,我们可以把稳态人均消费写为
c* = f(k *) -δk *
稳态的消费是在扣除了稳态折旧之后所剩余的稳态产出,该方程表明稳态资本的增加对稳态消费有两种相反的效应
- 更多的资本意味着更多的产出
- 更多的资本也意味着更多的产出必须被用于替换损耗的资本
下画出了作为稳态资本存量的函数的稳态产出和稳态折旧。稳态消费是产出与折旧之差。该图表明,存在一个使消费最大化的资本存量水平–黄金律水平
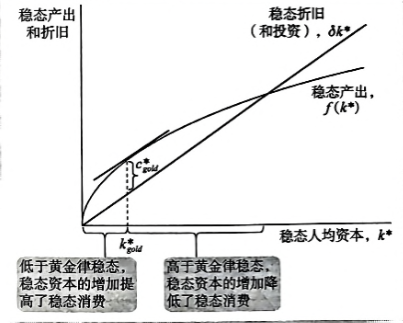
在比较稳态时,更高的资本水平既影响产出又影响折旧。如果资本存量低于黄金律水平,那么,资本存量的增加所引起的产出的增加大于折旧的增加,因此消费会上升。在这种情况下,生产函数比δk线陡峭。因此,两条曲线之间的距离等于消费——随着k的上升而增长。相反,如果资本存量高于黄金律水平,资本存量的增加减少了消费,这是因为产出的增加小于折旧的增加。在这种情况下,生产函数比 δk线平坦,因此,两条曲线之间的距离(消费)——随着k’的上升而缩小。在资本的黄金律水平,生产函数和δk线的斜率相同,消费位于其最高水平。
黄金律可以用这个方程表示:MPK = δ,在资本的黄金律水平,资本的边际产量等于折旧率。如果MPK- δ>0,那么资本的增加会提高消费,因此k必定低于黄金律水平。如果MPK- δ<0,那么资本的增加会减少消费,因此k必定高于黄金律的水平。当MPK- δ=0时(资本的边际产量减去折旧),那么我们就可以使用这一条件找出一个经济的黄金律资本存量。
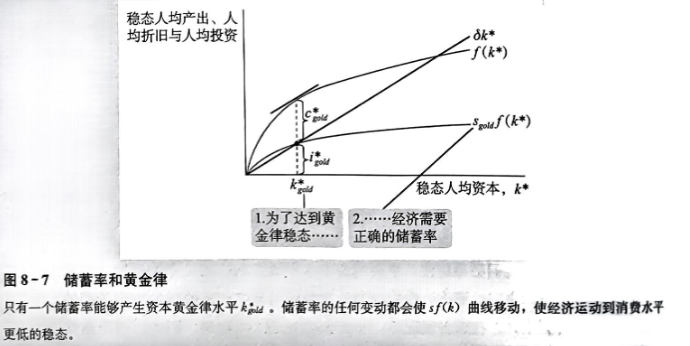
经济并不会自动地趋向于黄金律稳态。如果我们想要任何一个特定的稳态资本存量,例如黄金律水平,那么,我们就需要一个特定的储蓄率来支持它。图8-7显示了储蓄率被设定为产生黄金律资本水平的情况下的稳态。如果储蓄率高于该图所使用的水平,稳态资本存量就太高了;如果储蓄率低于这个水平,稳态资本存量就太低了。在任何一种情况下,稳态消费都低于在黄金律稳态的水平。
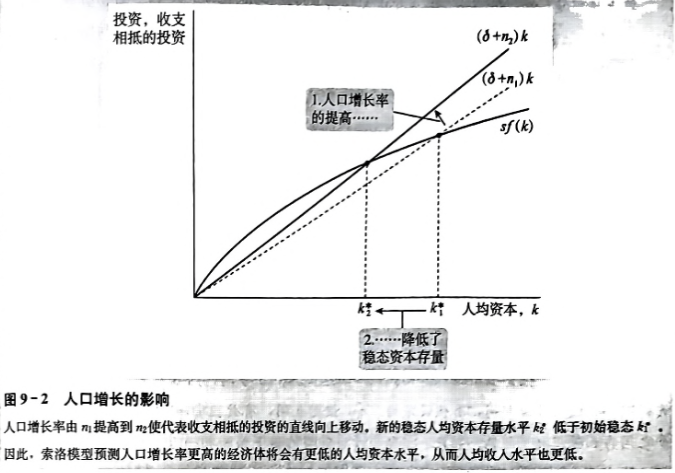
人口增长对索罗模型的影响
- 它让我们离解释持续的经济增长更接近
- 索洛模型预测人口增长率更高的国家将会有更低的人均GDP水平。注意,与储蓄率的变动一样,人口增长率的变动对人均收人有水平效应,但不影响人均收人的稳态增长率。
- 人口增长影响我们决定黄金律(消费最大化)资本水平的标准。
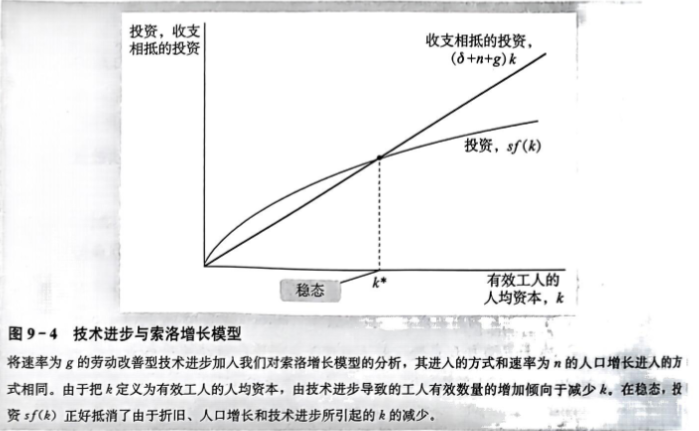
技术进步对索罗模型的影响
技术进步导致工人的有效数量增加。我们用k=K/(L*E)代表有效工人的人均资本,用y=Y/(L *E)代表有效工人的人均产出。利用这些定义,我们可以再次写出y=f(k)。表示随着时间变动的方程现在变为:
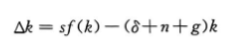

经济增长源泉的核算
生产要素的增加
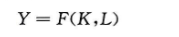
资本的边际产量(MPK)的定义:
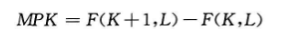
劳动的增加
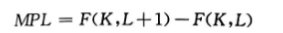
资本与劳动的增加
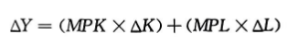
第一个括号中的项是资本增加所导致的产出增加,第二个括号中的项是劳动增加所导致的产出增加。这个方程向我们表明了如何把增长归因于每一种生产要素。现在我们想把最后一个方程变成更加容易解释的形式,并运用于可获得的数据。首先,通过一些代数整理,这个方程如下:
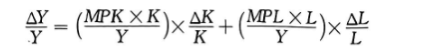
在生产函数为规模报酬不变的假设下,欧拉定理告诉我们,这两个份额之和为1。在这种情况下,我们可以写出:
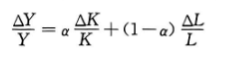
生产函数写为如下形式来包括技术变动的影响:
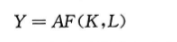
式中,A为技术水平的衡量指标,被称为全要素生产率。现在资本和劳动增加与全要素生产率的提高都会导致产出增加。如果全要素生产率提高 1%而投人保持不变,那么产出也增加1%。
将技术变动包括进来使我们的经济增长核算方程增加了一项(产出增长=资本的贡献十劳动的贡献十全要素生产率的增长):
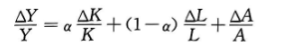
由于全要素生产率无法直接观察到,所以要间接地衡量。我们有产出、资本和劳动增长的数据;我们也有资本在产出中所占份额的数据。根据这些数据和增长核算方程,我们可以计算得到全要素生产率的增长;
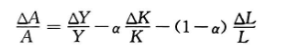
ΔA/A 是不能用投入变动解释的产出变动。因此,全要素生产率的增长是作为-个余量计算出来的:它是我们考虑了可以直接衡量的增长决定因素后剩余的产出增长量。
案例
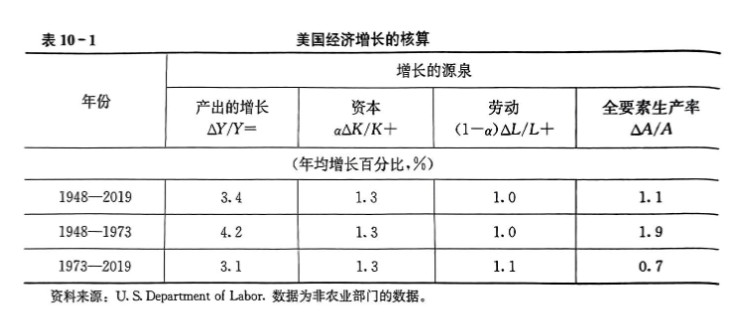
在了解了如何衡量经济增长的源泉之后,现在我们来看看数据。表10-1使用美国的数据来衡量 1948-2019 年间增长的三种源泉的贡献。
该表显示,在这一时期,非农产业部门的产出平均每年增长3.4%。在这3.4%中,1.3%是由于资本存量的增加,1.0%是由于劳动投入的增加,还有1.1%是由于全要素生产率的提高。这些数据表明,资本增加、劳动增加和生产率的提高对美国经济增长所做出的贡献几乎相等。
表10-1还表明,在1973年左右,全要素生产率的增长大大减缓了。1973年以前,全要素生产率每年增长1.9%;1973年以来,其增长率每年只有0.7%。经过多年的积累之后,哪怕是增长率的微小变动也会对经济福利有很大的影响。如果生产率增长率一直保持在原先的水平,2019年美国的实际收入将会比现实值高大约 70%。
为什么 1973年左右生产率增长会开始减缓呢?有许多假说解释这个现象。以下是其中的三个。
衡量问题 ,一种可能性是生产率减缓并没有真正发生,仅仅是数据存在缺陷。衡量通货膨胀的一个挑战是对产品与服务的质量变化进行校正。当衡量产出和生产率时也产生了同样的问题。例如,如果技术进步导致更多的电脑被生产出来,那么,产出和生产率的提高是易于衡量的。但是,如果技术进步导致运行速度更快的电脑被生产出来那么,产出和生产率提高了,但这种提高更为微妙和难以衡量。政府的统计人员努力校正质量的变动,但尽管他们做了最大的努力,得出的数据仍然远远不够完美。
无法衡量的质量改进意味着,我们的生活水平比官方数据所表示的提高得更快。这个问题应该让我们对官方数据有所怀疑,但这个问题本身并不能解释生产率的减缓。为了解释增长的减缓,我们必须证明衡量问题变得更糟。有理由相信可能是这样。随着时间的推移,在农业和制造业这样的生产产品的行业的就业减少了,这些行业的产出是有形的而且易于街量,在教育和卫生保健这样的服务性行业的就业增加了,这些行业的产出是无形的而且不那么容易衡量。但是,很少有经济学家认为衡量问题就是故事的全部。
工人素质的下降 一些经济学家提出,生产率的减缓可能是由劳动力的变动造成的。在20世纪 70年代初,大批“婴儿潮”一代离开学校并参加工作。同时,社会规范的变化鼓励许多妇女改变全职家庭主妇的角色和进入劳动力队伍。这两种新情况都降低了工人的平均经验水平,从而降低了平均生产率。
另一些经济学家指向了由人力资本来衡量的工人素质的变化。虽然劳动力的受教育程度在这一时期一直在提高,但在最近几十年提高得并不像过去那样快。此外,一些标准化考试的成绩下降表明教育质量在下降。这两个因素都可以解释生产率增长的减缓。
思想的枯竭 有一些经济学家提出,20世纪70年代初,世界上关于如何生产的新思想已经开始枯竭,使经济进入了一个技术进步减缓的时代。这些经济学家常常认为,这种异常情况不是 20世纪 70年代以来的生产率增长减缓,而是在此之前的20年里(即20世纪50年代和 60年代)生产率增长的加速。在20世纪40年代末,经济中有大量由于20世纪30年代的大萧条和 40年代上半期的第二次世界大战而未能充分实施的思想储备。这种论证继续说在经济用究这些思想储备之后,生产率增长减缓就是可能的了。的确,尽管1973 年以后的增长率与 20世纪50年代和 60年代相比令人失望,但并不比1870-1950年的平均增长率低。不幸的是,生产率增长的减缓仍然是一个谜。在20世纪90年代中期,生产率增长加速了,这一新情况常常被归功于计算机和信息技术的发展,但事实证明生产率增长加速只是暂时的。在 21世纪 10年代,全要素生产率的增长率只有每年0.7%。始于1973年左右、令人难以理解的生产率增长减缓仍然是当代经济的特征之一。
