哈夫曼树

哈夫曼树的基本概念

路径：从树中一个结点到另一个结点之间的分支构成这两个结点间的路径

结点的路径长度：两结点之间路径上的分支数

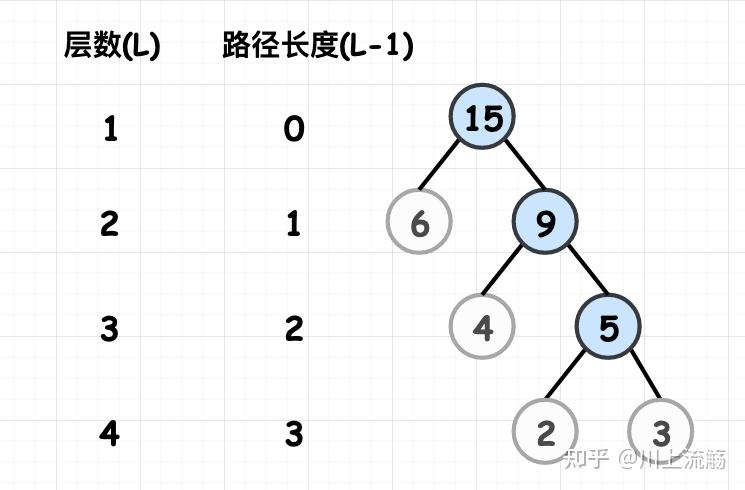
树的路径长度：从树根到每一个结点的路径长度之和．记作：ＴＬ

权（weight)：将树中结点赋给一个有着某种含义的数值，则这个数值秒针为该结点的权

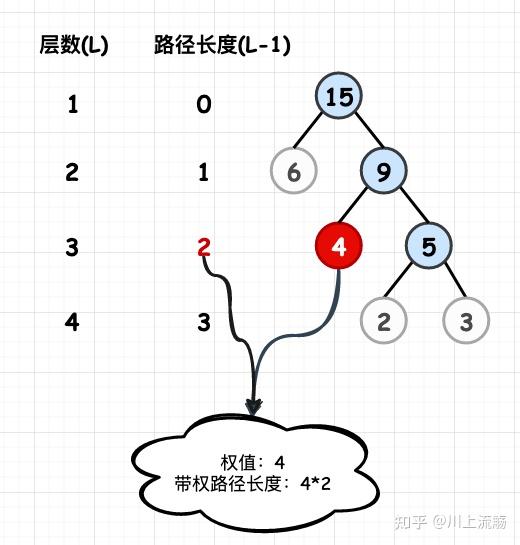
结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积

树的带权路径长度：树中所有叶子结点的带权路径长度之和．记作:WPL(Weighted Path Length)

哈夫曼树：最优树（带权路径长度（ＷＰＬ）最短的树）

image-20250323085954263

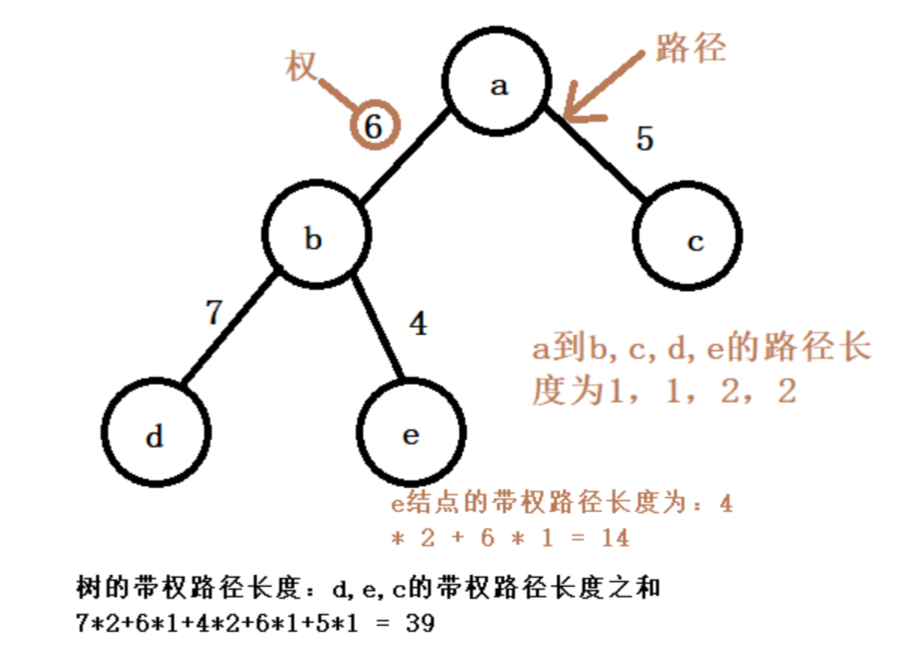
哈夫曼树：最优二叉树

特点：

１满二叉树不一定是哈夫曼树．

２哈夫曼树中权越大的叶子离根越近．

３具有相同带权结点的哈夫曼树不惟一．

构造哈夫曼树的方法

哈夫曼树的实现利用了贪心算法的理念，就是先给定的若干结点的权进行分割，让它们变为单个的森林或者说是单个的树，因为树肯定是森林，而后在其中选择两个权值最小的结点生成新的结点，而后删除被选择的结点，让生成的结点参与森林中进行选拔，直至无结点进行选拔。

步骤

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

例题

例题：已知结点权值的集合为w(2，3，4，6)求其哈夫曼树

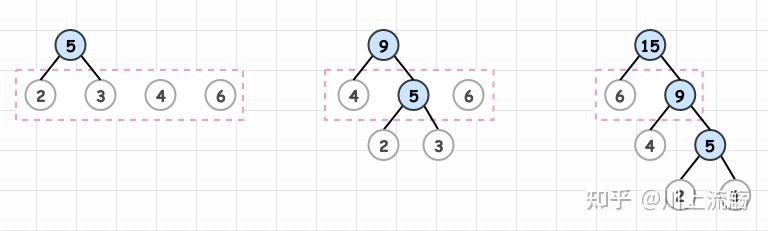
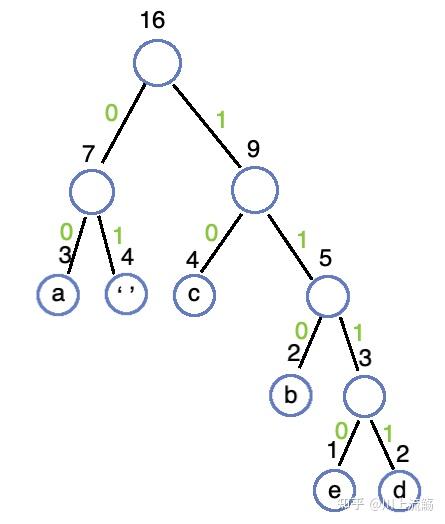
哈夫曼树编码

左分支为0，右分支为1，标记后将从根到叶子结点的路径上标记的0和1收集起来，得到叶子结点对应的字符的具体编码，这就是哈夫曼编码。

image-20250323100115884

代码实现

哈夫曼树实现思路

1. 定义 HuffmanNode 结构：
   • 代表哈夫曼树的节点，包括字符 ch 和权重 freq。
   • 左右子节点 left 和 right 用于存储树结构。
2. 使用优先队列 (std::priority_queue) 作为最小堆：
   • priority_queue 按照 最小频率优先 进行排序。
3. 构造哈夫曼树：
   • 将所有字符和权重插入最小堆。
   • 取出最小的两个节点，合并成一个新节点并重新插入最小堆。
   • 直到堆中只剩下一个根节点，哈夫曼树构造完成。
4. 生成哈夫曼编码：
   • 递归遍历树，左子树路径为 "0"，右子树路径为 "1"，最终生成哈夫曼编码表。
5. 输出编码结果：
   • 遍历 unordered_map<char, string>，打印编码结果。

复杂度分析

• 最小堆操作（插入、删除）：每次操作O(log⁡n)。
• 构建哈夫曼树：有 n 个字符，需要进行 n−1 次合并，每次合并操作的复杂度为 O(log⁡n)，因此整体复杂度是 O(nlog⁡n)。

使用场景

• 文件压缩（文本编码）
• 数据传输优化
• 信息熵计算

具体代码

结构体定义

none

#include <iostream>
#include <queue>
#include <unordered_map>
#include <vector>

using namespace std;

// 哈夫曼树的节点结构
struct HuffmanNode {
    char ch;
    int freq;
    HuffmanNode left, right;
    
    HuffmanNode(char ch, int freq) : ch(ch), freq(freq), left(nullptr), right(nullptr) {}
};

优先队列比较函数

none

// 优先队列的比较函数
struct Compare {
    bool operator()(HuffmanNode a, HuffmanNode b) {
        return a->freq > b->freq; // 小顶堆
    }
};

递归构建哈夫曼编码

none

void generateHuffmanCodes(HuffmanNode root, string code, unordered_map<char, string>& huffmanCodes) {
    if (!root) return;
    
    if (!root->left && !root->right) {
        huffmanCodes[root->ch] = code;
    }
    
    generateHuffmanCodes(root->left, code + "0", huffmanCodes);
    generateHuffmanCodes(root->right, code + "1", huffmanCodes);
}

构建哈夫曼树并构造其编码

none

// 构造哈夫曼树并生成编码
unordered_map<char, string> buildHuffmanTree(const unordered_map<char, int>& freqMap) {
    priority_queue<HuffmanNode, vector<HuffmanNode>, Compare> pq;
    
    // 1. 初始化最小堆
    for (auto pair : freqMap) {
        pq.push(new HuffmanNode(pair.first, pair.second));
    }
    
    // 2. 构造哈夫曼树
    while (pq.size() > 1) {
        HuffmanNode left = pq.top(); pq.pop();
        HuffmanNode right = pq.top(); pq.pop();
        HuffmanNode newNode = new HuffmanNode('\0', left->freq + right->freq);
        newNode->left = left;
        newNode->right = right;
        pq.push(newNode);
    }
    
    // 3. 生成哈夫曼编码
    unordered_map<char, string> huffmanCodes;
    generateHuffmanCodes(pq.top(), "", huffmanCodes);
    
    return huffmanCodes;
}

调试

none

int main() {
    unordered_map<char, int> freqMap = {
        {'a', 5}, {'b', 9}, {'c', 12}, {'d', 13}, {'e', 16}, {'f', 45}
    };
    
    unordered_map<char, string> huffmanCodes = buildHuffmanTree(freqMap);
    
    // 输出哈夫曼编码
    for (auto pair : huffmanCodes) {
        cout << pair.first << ": " << pair.second << endl;
    }
    
    return 0;
}