引言
作者论述了一下亲身学习的经历,比较了为什么要选择国外的数学教材的原因
如何理解曾博所说的“看国外数学教材提高智商”?
首先需要
他老人家,这样说错了就可以打黑猫的脸,然后赶紧改正了
这一点作为七本失败文科垃圾,在国内本科尝试自学数学(90%)失败,后在国外五本补上部分数学基础的黑猫是有部分有发言权的。(这里跑题了。说的是国外大学教材,但是道理是一样的)
很多人问黑猫,你干嘛在美国数学这么“垃圾”的地方学数学。先不吐槽美国数学“垃圾不垃圾”这个问题,首先要明确的是,国内有很多优秀本科数学教材和译文,比如:数分张筑生,线代蓝以中,泛函侯有良,西安交大工程复变, 上财译版Steven Shreve。假设即使有无良老师兜售自己的教材,在挑选好教材后依然可以继续学习。但是为什么作为文科四流专业的垃圾黑猫,偏偏在国内数学学不下来,到了“垃圾”的美国反而学会了呢。难道是用七本文科的垃圾数学去吊打“垃圾”的美国人了么,非也非也…… 其中有几个问题,既可以说是国情差异,也可以说是教学差异。
国内教材:
1.国内教材继承老派苏系数学教材,以传统的定义-逻辑路线,加之大量的熟练性,技巧性习题进行教学。这种教学是无可厚非的,因为这些都是非常重要的基础,黑猫自己就吃了自学没有练够的亏。但是这种教学方法不能说是完全没有问题的。首先某些过于抽象的概率在定义-逻辑路线下几乎是不可读的。(举个例子,sigma-algebra,在一开始用信息集意义讲解和传统集合论的方式讲解难度差别可以类比文明五的酋长和天神的差别)。智商比较一般的失败学生(比如我)一旦同时缺乏向死而生自残精神,容易直接被秒杀。多次之后积极性严重受挫彻底放弃学习数学。其次,大量技巧性的“神凑”,“天凑”,“鬼凑”,“荒天凑”,“史诗凑”,“传说凑”(等“显然的”变量代换),虽然对数学的学习很重要(黑猫自己吃了亏),然而这些确实也不是学习数学的全部。对这一方面的过度重视确实不太利于”天赋树“的形成。(当然,成功的数学人士完全可以认为黑猫是因为笨,懒,废物,题做得少而导致这些的,黑猫完全接受这些批评)
2.基于1的特征,国内的数学考试(尤其是考研),再加上国内考试重要的筛选性性质。会进一步(无论在课上还是教材上)重视基础学科(比如数分)学习上的“神凑”,“天凑”,“鬼凑”,“荒天凑”,“史诗凑”,“传说凑”。学生会在某重程度上进一步加强这些训练,而忽视“天赋树”的形成。(同样,黑猫完全接受关于笨,懒,废物,题做得少的批评)
3.由于教材的1和2特征,在一些“天赋树”至关重要的内容上。部分国内教材,教学进度(和考试需求)上能会因为对“神凑”,“天凑”,“鬼凑”,“荒天凑”,“史诗凑”,“传说凑”的需求,而导致对重要的天赋树节点不够重视。这一点不能说无可厚非了,因为各个领域的同学表示很多教材这个问题已经相当严重了。比如在复分析中傅立叶积分变换的教学中,对希尔伯特空间和投影等至关重要的概念不够重视,大量训练傅里叶级数的三角变换技巧和复积分技巧,导致最后难以理解其线性变换的本质。又比如在量子力学中,对复向量和酉变换等至关\重要\概念不够重视,大量训练复化的波动方程(你们知道我在说什么,应该出现在数学物理方法这门课里,而不是量子力学里)求解,导致学生淹没在偏微分方程的求解中而丢失方向
美国教材(或公开课):
相比之下,美国公开课或教材与国内一般教材最大的不同是也对应上面的特征:1.非常重视天赋树;2.以概念掌握和例子为主,配合习题;3.对于重要的抽象概念,暂时放弃数学严谨性,以给予读者理解为优先级的情况下后将严格概念补上,或在更高等教材和课上补上。
对于这三点,黑猫印象最最深刻的例子,就是学习复分析中重要内容柯西-黎曼方程时,同时使用国内优秀教材西交大工程数学复变函数和著名教材“Visual Complex Analyst” ,同时体现了这三点多差异。
我们先看国内教材:


对不对,对极了。利用复微分的定义分实部虚部求导正出充分性(必要性用条件导出deltaZ的极限证出)。但是黑猫笨啊,蠢啊,失败啊。我除了看懂这个证明的每一步之外对这个条件“本质”完全一无所知啊~
再看美国教材:
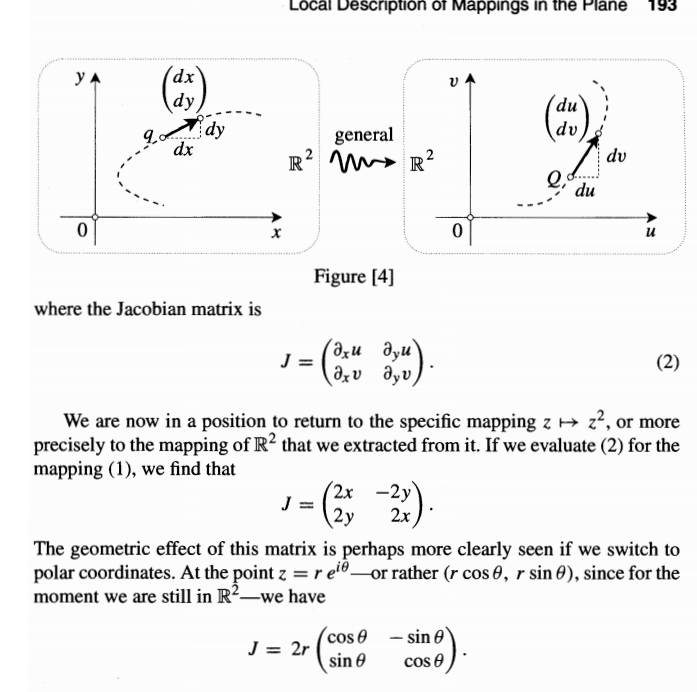
先写出一个二维向量的雅可比矩阵,然后提取模长之后导出代表向量角的雅可比矩阵

然后暂时“放弃”严谨性,告诉我们。解析有个非常好的性质(充分条件):保角变换,同时花了图,直观地告诉我们保角变换的意思指,该函数不会改变向量集里两向量之间的夹角

然后,再“放弃:一点严谨性,告诉我们这里的保角性等价于解析(到这里,好奇的人就会开始想为什么)

最后给出柯西-黎曼方程的时候恍然大悟,因为保角性“保住了”映射时向量的角(雅可比矩阵)。角被“保住了”后,函数的值的雅可比矩阵真的显然能推出是柯西-黎曼方程(对应一开始角的雅可比矩阵)
这一举,不但直观明了柯西-黎曼方程,给了极好的例子,在讲的过程中以保角为主线,顺便一路开枝散叶了很多拓扑里的东西。而在这个时候, 竟然还没严格提出共形映射(用保角映射代替了)。虽然”暂时“丢失了严谨性,但是哪个更加透彻不言而喻。
这样的讲解,显然是比直接去练习20道求导题深刻的,黑猫虽然没有去练神凑,但是智商确实已经+1
总结:
也说是国情,也说是无奈。在国内没有时间和机会对数学这样理解,也没有时间去将这些看起来没啥用的”本质“的东西。也许是因为“神凑”,“天凑”,“鬼凑”,“荒天凑”,“史诗凑”,“传说凑”,他们难,能练出扎实的分析功底,也能筛选出人才。但是从自学者,或者初学者的角度。有多少人能经受住这些“凑”们的攻势,又有多少人能在这些猛烈进攻下理一理没用的“天赋树”,学一学有趣却没用的本质呢。作为一个自学数学的文科失败者,没有足够的训练导致实力的垃圾和黑猫也是不幸和愚蠢和可悲,但是自学过程那些(自以为)+1+1+1的智商也是某种幸运吧
反正是个失败的金融矿狗,再怎么学这些都是失败的
彩蛋:
由于几个月前,的一个失败的flag:

黑猫还真的跟一个智障一样,失败地去学习量子力学了
在努力学习过英语的基础下,黑猫同时观看stanford量子力学公开课,wiki百科薛定谔方程,外加
李大嘴博士的悉心指导下,黑猫尝试卖了个叠加态的萌(顺便批判曾谨言,明明可以从线性代数的角度讲清楚的事情干嘛要一上来就搞PDE啊,还tm是复化的!):

在物理大神观测(打脸)之前,黑猫不知道哪里有什么硬伤,卖萌处于|成功》和|失败》的叠加态。兴趣使然浪费时间,如果有错误,欢迎大神们观测(打脸)。观测完后有助黑猫知道自己是圆是扁,从而能够更加流畅地继续兴趣使然浪得时间。
不知道算不算对各种Boism 理论进行了实践
