本科三件套的高数（微积分），线性代数，初等概统我就不推荐举例子了，反正看哪本都差不多，写的一样烂，值得一提的是本科线性代数我强烈推荐b站搜索网课《俗说矩阵》
高等代数/矩阵论/矩阵分析：算是最核心的一本书，个人推荐先看《线性代数应该这样学》再去看方保镕的《矩阵论》；这两本书中学到的关于谱分解定理，矩阵各种分解，基向量正交，范数等内容将会成为后面的基础（特别是当各位接触中高级计量经济学时，多元回归必然要引入矩阵分析）；特别指出的是对于学习数学我们有”气宗“和”剑宗“两种路径，前者意味着更倾向于数学的分析性数学本身，后者就是我这种半吊子搞应用的，如果你有志于成为气宗弟子那这里推荐丘维声的高等代数，方保镕的矩阵论本质是应用工具书。
数学分析：我等剑宗弟子可以直接跳过了(
运筹学/凸优化：这里运筹学我直接推荐清华大学出版社的那本《运筹学》，里面会从单纯形法，整数规划一直讲到动态最优化，足够把高等宏观经济学啃下来了；至于为什么不推荐凸优化的课程，单纯是因为搞经济学和金融应用的大概率用不到，我相信没有哪个人做DSGE模型的时候还要证明那一堆凸集，强对偶性质。
当然，你说主播主播，你的剑宗秘诀虽然很偏应用，但还是太难了，有没有不吃数学功底的打法。有的兄弟，有的，立马推：【【运筹学】应试向基础教程（已完结）{适用范围：本科期末、考研、考博}】https://www.bilibili.com/video/BV1Uw411f7WM?vd_source=8861e50b2ff132744cc16c64dcbed7f7
点集拓扑：熊金城的《点集拓扑讲义》即可，需要注意的是这本书面向的是本科生阶段的拓扑学内容，真正的核心其实是P179的布劳威尔不动点定理和约尔当分割定理，而受限于本科阶段所以它只证明了二维空间上的不动点存在。当然，看完到这里也基本够各位把MWG，约翰罗默的《马克思主义经济学分析基础》这类高等经济学啃下来了。
实变函数/测度论：推荐程士宏的《测度论与概率论基础》，为啥选这本小册子呢，有两个原因：第一是它对我们这种搞应用的人来说足够轻便和紧凑，不会讲太多与主线无关的分析性质证明。第二点是因为光看实变函数反正你看哪本都一样，完全不知道自己在干嘛，也不知道有什么用，还不如快点把R-N导数，三一律这些东西学完然后开始下一阶段学习。这里建议看完后再配合汪林的《实分析中的反例》，要多思考多自己构造反例。
高等统计学：这里推荐郑国忠的《高等统计学》和赵林城的《高等统计学概论》对照着看。
实际上到了这里才能真的理解实变函数中那一堆东西在干嘛，比如有了R-N定理我们可以在只证明了测度结构的情况下写出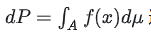
这样的式子，不再需要微分算子具有的线性结构，面对诸如布朗运动这种处处连续处处不可导的玩意就有了将其”测量“的方法。然后用这样的方式去再反过来把初等概统中的各种概念放在更高维的视角中理解，也同时能解答各位学初等概统时的疑问：这沟槽的卡方分布，t分布，F-分布到底是怎么来的。
至于推荐上面两本书对照着看，是因为《高等统计学》这本书相对《高等统计学概论》更”初等“，它会不厌其烦用一些更好理解的方式去举例子给读者，但是也更需要计算能力。而后者更视角”高等“也更加抽象，全是各种定理证明，两者对照看更好理解实变函数中那一堆东西到底在说什么（至于fubini定理，Holder不等式这种东西，我觉得各位都学到这里了，应该都是把计算的事情交给计算机吧）
随机分析：推荐Richard写的《随机过程基础》和王军写的《随机过程及其在金融领域中的应用》
第一本《随机过程基础》真的是神中神的一本书，它在不引入任何矩阵分析，测度论的前提下一路给读者讲到了B-S期权定价模型和鞅理论，是我读过感觉最好的一本数学书，学完本科数学三件套即可阅读。而且这本书的涵盖内容基本上把经济学需要用到的随机分析问题都覆盖了，比如很经典的经济学蛛网模型，本质就是更新过程在离散时间下的低维退化，还有各种生灭问题变形，ABM随机等内容。
第二本《随机过程及其在金融领域中的应用》写的很烂，但是优点是足够紧凑，看完第一本可以拿来对照着看，这样能理解测度论视角下的随机分析问题在初等视角下应该如何理解。
看完这两本就可以去尝试更高阶的，真正完全在测度论视角下分析随机的书了。
剩下的就是一些纯工具书，比如离散数学，常微分方程，买哪本都一样，哪里不会看哪里就行，没必要通读
