初等基本函数
基本概念
映射：没什么好说的
定义域D：一般来讲它是一个区间
值域I：f(x)求值的范围
一般来说D和f去定了，I也就随之确定了，一个函数最核心的要素就是D和f
单值函数与多值函数
只有1对1，或多对一的函数，我们成为单值函数。一对多我们称为多值函数。
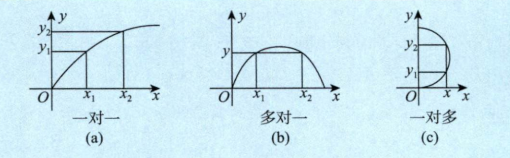
求函数值域的思路
对于连续函数f(x)，只需要求出f(x)的最小值m和最大值M，值域I=[m,M]
特殊情况
取不到最大值：，值域I=（0,1）
单调性
相同单调增加，相反单调减少（同增异减）
奇偶性
奇函数的定义：
奇函数的图像是关于原点对称的
偶函数的定义：
偶函数图像是关于x方向对称的
幂函数：如
对数函数：是幂函数的反函数，例如
复反函数：
例如：
结论：单调函数一定有反函数，且单调的原函数与其反函数单调性相同
周期函数：略
例题
反函数
注意：这种叫做双曲正弦函数，它是偶函数，是一种特殊的悬链线
,这种叫做双曲余弦函数
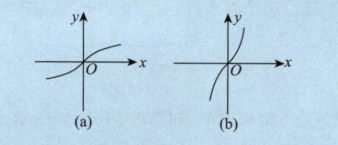
复合函数
设函数y=f(u)的定义域为，函数u=g(x)在D上有定义，且确定的函数称为由函数u=g(x)和函数y=f(u)构成的复合函数，它的定义域为D，u称为中间变量
解题思路：
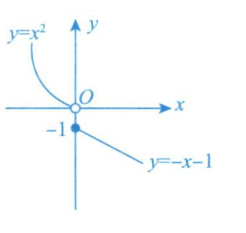
解析：注意命题的包装，
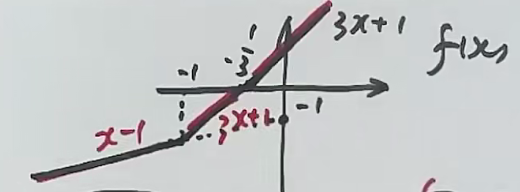
注意：
