微积分01:微积分前置基础

数学 微积分
数学
发布日期:   2025-01-14
更新日期:   2025-04-27
文章字数:   3.2k
阅读时长:   11 分
阅读次数:   8

前言

中学基础，迅速过一遍吧…Latex语法调markdown语法折腾了一下午，麻了，凑合着看吧。什么？看不懂！？一头创死算了！！！

绝对值

的定义为：既当,绝对值等于原值，当a<0时，绝对值等于原值的相反数

集合

一般来说⊆表示包含（两个集合可能相等），⊂表示真包含（两个集合不能相等）

基本概念

元素聚合起来便是集合

若属于，表示为若不属于，表示为

常用的实数集

  1. N:全体自然数构成的集合
  2. : N{0}，正整数集(N去掉0就是)
  3. Z：全体整数构成的集合
  4. Q：全体有理数构成的集合
  5. R：全体实数集合
  6. I：全体虚数集合
  7. C：全体实数和虚数组成的复数的集合称为复数集

有理数和实数具有稠密性

即：

对于任意，一定存在，对于任意，一定存在

集合的表示法

1、例举法
Missing or unrecognized delimiter for \left \left{ 0 \right},\left{ -1,0,1 \right}
2、描述法
Missing or unrecognized delimiter for \left \left{ x \mid 0 < x < 1 \right}

研究集合A与集合B的关系

若集合A包含于集合B，表示为

若，则，都有

注：若，，则

集合相等且从而，若要证明A=B，只需证且

空集：无任何元素的集合

注：集合，，

集合运算

并∪：A∪B={x∈A或X∈B}

  1. A∪B=B∪A
  2. A∪A=A
  3. A并∅=A
  4. A(A∪B)，B(A∪B)
  5. ABA∪B=B

交∩：Missing or unrecognized delimiter for \left A∩B=\left{ x\in A且x\in B \right}

  1. A∩B=B∩A
  2. A∩A=A
  3. A∩=
  4. A∩BA，A∩BB
  5. A

若一个集合含有所研究问题中涉及的全部元素，就称这个集合为“全空间”，记作,概率论中的全概率公式会用到

补集：

  1. A∩(B∪C) = (A∩B)∪(A∩C)
  2. A∪(B∩C)=(A∪B)∩(A∪C)

区间

(a,b)={x|a<x<b}

Missing or unrecognized delimiter for \left (a,b) = \left{ x|a<x<b \right}

Missing or unrecognized delimiter for \left [a,b) = \left{ x|a\leq x<b \right}

Missing or unrecognized delimiter for \left (a,b] = \left{ x|a< x\leq b \right}

Missing or unrecognized delimiter for \left [a,b] = \left{ x|a\leq x\leq b \right}

特殊的：Missing or unrecognized delimiter for \left R=\left{-\infty,+\infty \right}

区间是集合，而不是不等式。

命题

充分条件和必要条件

p,q是命题

例：，则，称为的充分条件，为的必要条件

释义：

充分条件

如果是某种条件，且可以推导出必成立，那么我们可以说是的充分条件，因为如果成立（即），那么必定成立（即）

必要条件

如果成立时必须成立，即条件成立时也一定成立，则是的必要条件。

总结：如果某个事项可作为另一个事项满足的条件，但非必须，可以有替代则称该条件为充要条件。如果某个事项必须由它满足，则称该事项为必要条件。

常用的充要条件：或者（同号）

或者（异号）

全称量代词：和存在量词

设p(x)是与x相关的命题

全程命题：，，例

存在命题：例：

如何对命题进行否定

例：原命题：真否定：假

对命题进行否定时，

、

、

否定规则总结：

符号 ¬ 表示 逻辑否定，即“非”或者“不是”

  1. 量词的否定：
  2. 关系符号的否定：
    • ¬(a=b)≡a≠b
    • ¬(a>b)≡a≤b
    • ¬(a<b)≡a≥b

逆否命题

若p，则q的逆命题为若q，则p

逆否命题的真假与原命题一致，即若，为真，则为真

要证明为真，只需先否定结论再推出

举例：

假设原命题为：

  • 原命题：如果下雨，则地面湿。
    • p: 下雨
    • q: 地面湿

原命题的符号表示为：p⇒q

逆命题是：¬q⇒¬p

即“如果地面不湿，则没有下雨”。

示例解释：

  • 原命题：如果下雨（p），则地面湿（q）。
  • 逆否命题：如果地面不湿（¬q），则没有下雨（¬p）。

逆否命题的符号：

  • 如果原命题为 p⇒q，那么其逆否命题为：

¬q⇒¬p

它的符号表示就是“¬”和“⇒”组合起来。

基本算术公式

平方差公式

平方差公式

十字交叉公式

幂的运算规则

注意：不一定成立，例如：注：，

练习

化简：

解：第一步：化简分子第二步：化简分母第三步：分子除以分母

指数的运算规则

为什么对数恒等式变形成立？

和平方与开方互为反运算是一个道理同样地，当你取一个正数a>0，它的自然对数是，再对它取指数就会返回原数：即

练习

例对做对数恒等变形。

设：对数有乘法转加法的性质

算数几何平均不等式

当，

恒等式

不等式

如何比较两个数的大小？

例：，比较与两者的大小

方法1：作差法

解：当结果大于等于时，说明大于另一方或者等于另一方

方法2：作商法

解：因此，当除于结果大于或等于时，说明前者比后者更大

方法3：平方后作差

解：均大于，最后的结果式子可得也大于或等于

最值

情景1：已知x>0,y>0，xy=a，求x+y的最小值

解：当时，取最小值

情景2：已知x>0，y>0，x+y=b，求xy的最大值

解：当时，最大值为

运用不等式进行转化：然后取倒数得到：然后两边乘以，可得：因此，可以推出：

例:，求的最小值

思路：先构造出a>0，b>0

解：当现在式子分割成了两部分，设，此时的式子变成了，再运用求解可得：，即由上述可知，当且仅当时，等号成立因此最小值是，的最小值是。所以最小值是

一元二次方程

、当时，方程有个实数根、当时，方程有个实数根、当时，方程没有实数根求根公式：

韦达定理

设的两根为，，则，

初等基本函数

基本概念

映射：没什么好说的

定义域D：一般来讲它是一个区间

值域I：f(x)求值的范围

一般来说D和f去定了，I也就随之确定了，一个函数最核心的要素就是D和f

单值函数与多值函数

只有1对1，或多对一的函数，我们成为单值函数。一对多我们称为多值函数。

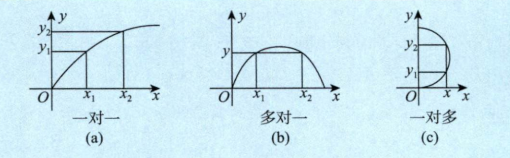
求函数值域的思路

对于连续函数f(x)，只需要求出f(x)的最小值m和最大值M，值域I=[m,M]

特殊情况

取不到最大值：值域，值域I=（0,1）

单调性

相同单调增加，相反单调减少（同增异减）

奇偶性

奇函数的定义：且

奇函数的图像是关于原点对称的

偶函数的定义：且

偶函数图像是关于x方向对称的

幂函数：如

对数函数：是幂函数的反函数，例如

复反函数：作复合函数，或，则称与互为反函数，记

例如：

结论：单调函数一定有反函数，且单调的原函数与其反函数单调性相同

周期函数：略

例题

例题：设，则等于？

解：设，由题意可知，求，即函数输入的变量为，

例题：设函数的定义域为且满足，则等于？

解，设定量替换：定义域，由式可得，此处由于定义域是明确的，因此分母不取绝对值因此通分后可得式：联立方程组消元法求解：从方程解出将上述表达式代入方程化简后可得：

例题：给定，求

解：由题意可得方程组：那么式可得，将得到的结果带入式，可得：最后可得：

例题：，求

解：由题意可得式用消元法将式代入式可得式式：

反函数

例题：求函数的反函数的表达式及其定义域

运用指数运算的法则和共轭式子求解：，再由的表达式，可得出最后有式减去式，可得：，交换上式中的位置后就是的反函数，即，

注意：这种叫做双曲正弦函数，它是偶函数，是一种特殊的悬链线

,这种叫做双曲余弦函数

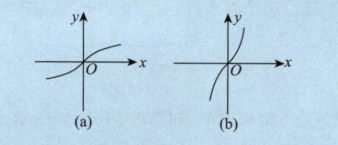
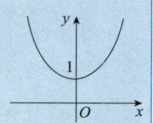
复合函数

设函数y=f(u)的定义域为，函数u=g(x)在D上有定义，且，则由确定的函数称为由函数u=g(x)和函数y=f(u)构成的复合函数，它的定义域为D，u称为中间变量

例题：设，，且，求及其定义域与值域

解题思路：看作

解：由题意条件可得，知的定义域为又它的根号情况下必大于等于当时，为最大值，显然为最小值。故的值域为

例题：设，，则

解：利用数形结合，画出里层函数图形，由图像可知：，故，

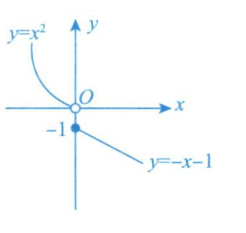
例题：设，则

解析：注意命题的包装，

解：，那么就会有，，，最终复合函数完整的表达式为，，，

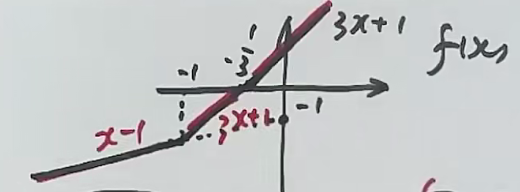
注意：

绝对值的关键在于内部表达式的符号，当时即，这是绝对值从正变负的临界点因此，数轴分割为两个区间：绝对值保持原数值绝对值取相反数

几何向量

  1. 曲线、直线、曲面、平面、空间提都是由点构成的，换句话说就都是点的集合
    1. 3个不共线的点可以确定一个平面
    2. 若一条直线的两个点都在一个平面内，则这条直线在这个平面内
    3. 若两个不重合的平面有一个公共点，则它们有且仅有一条过该点的交线
    4. 若直线L1平行于L2，L2平行于L3，那么就可以得出L1平行

推论1：一条直线及直线外的1点可以确定一个平面

推论2：2条相交直线确定一个平面

推论3：2条平行直线确定一个平面

  1. 三维空间中的点有3个自由度，x,y,z，对点p(x,y,z)若不加以约束，P可以出现在三位空间的任意地方

空间几何体

多面体、旋转体

柱体体积 V=sh

锥体体积 =

球体表面积

球体体积积

向量

三角函数

给定一个三角形：，，锐角为

基于上述关系，我们可以推出三角恒等式：

任意三角函数均已为周期

诱导公式

和角公式

倍角公式

三角有理积分常用的公式

余弦定理

正弦定理

同角关系

万能公式

辅助角公式

，其中满足

例题

用万能公式化简

解：设将万能公式带入原式可得：通分分子：分母整个式子就变成了：

反三角函数

当时，将的反函数定义为反三角函数，将的反函数定义为反三角函数

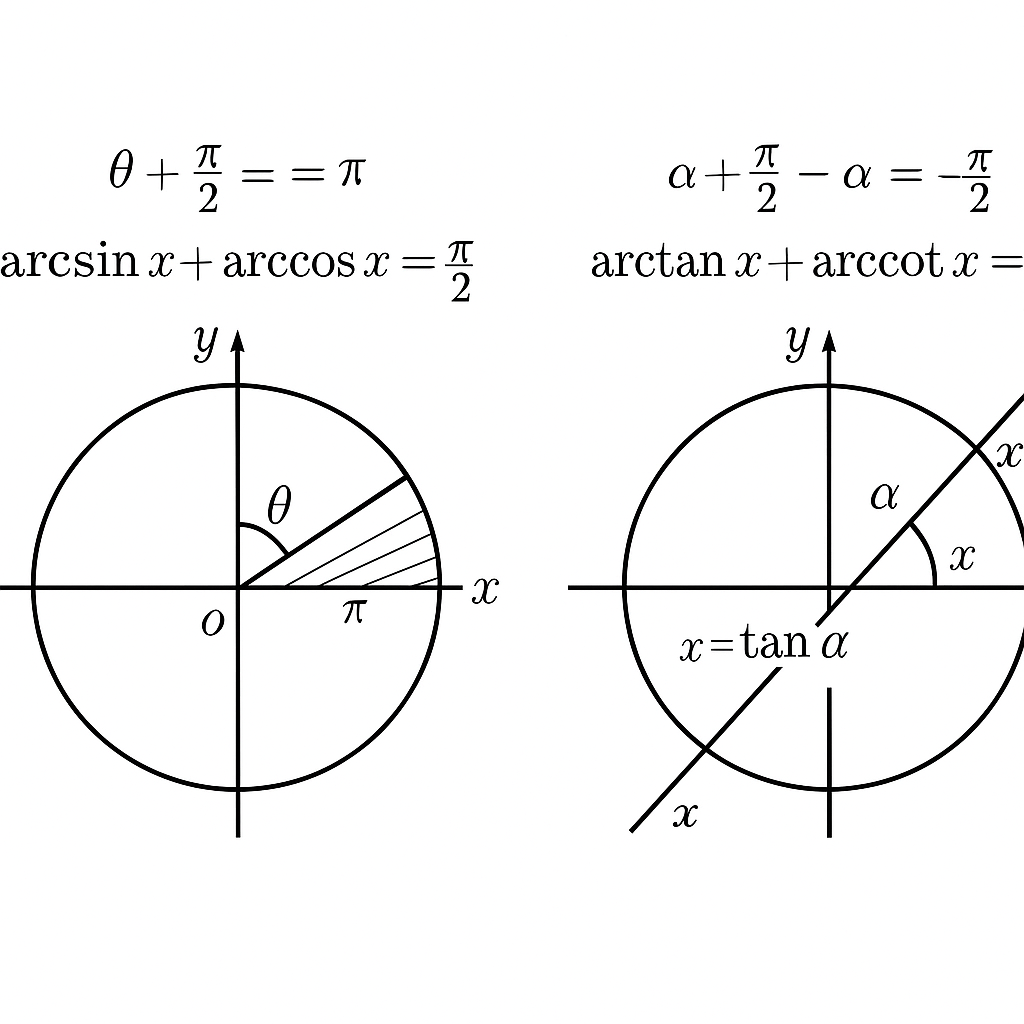
当时，将的反函数定义为反三角函数，将的反函数定义为反三角函数

例题2：，

证明：，设那么，由于，因此：既：

证明：设我们知道：所以两个恒等式都成立

数列

  • 等差数列：
    • 递推公式：
    • 通项公式：
    • 前n项和：
  • 等比数列
    • 递推公式：
    • 通项公式：
    • 前n项和：，，

数学归纳法

数学归纳法是一种数学证明的方法，通常被用于证明某个命题在自然数范围内成立，其一般步骤如下：

第一步：验证n取第一个自然数时成立

第二步：假设n=k时成立，然后以验证的条件和假设的条件作为论证的依据进行推导，在接下来的推导过程中推导处理在n=k+1时假设的原式成立

最后一步总结表述

例题

证明：

证明：第一步，取验证是否成立左边：，右边：，成立第二步，归纳假设，当时，等式成立第三步：归纳到要证明：首先提取公因式和通分合并将右边写成以为分母的情况：最终可得：所以最终表达式为：，成立

例题2:设，，证明数列是单调递减的数列

证明：对于所有的，都存在解题思路：只要能证明对于成立，那么整个数列就一直在变小，自然就是单调递减由于，这也就说明了是严格单调递减的

另一种解题思路

考虑函数，对它求导：，在，，也就是单调递增。又，当时，，即

参考资料

普林斯顿微积分读本

维基百科

文章作者: Gustavo
文章链接: https://gustavo1841.github.io/2025/01/14/shu-xue/wei-ji-fen/01-wei-ji-fen-ji-chu/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY-NC 4.0 许可协议。转载请注明来源 Gustavo !
数学 微积分
评论
0 comments
Anonymous
Markdown is supported

Be the first person to leave a comment!