04-5-按磁盘和外壳划分的体积

按磁盘和外壳划分的体积

磁盘和外壳

我们将通过一个例子来说明求体积的两种方法。

示例 1. 女巫的坩埚

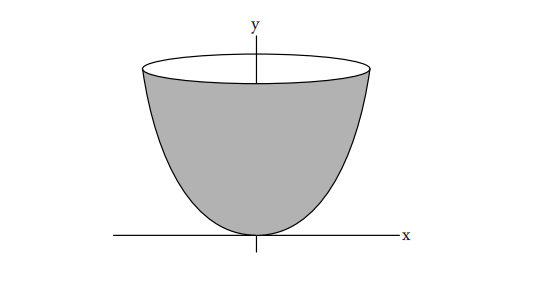
方法 1：磁盘

图 2 中磁盘的面积是 。
磁盘的厚度为 ，体积为 。
坩埚的体积 为

如果 米，那么 给出

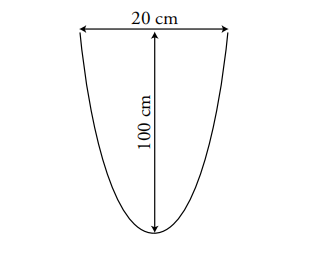
关于单位的警告

如果 a=100 厘米，那么

但是 。为什么这个答案不同？这个悖论的解决办法隐藏在方程中。

在顶部， 厘米。所以第二个坩埚看起来像图 3。相比之下，

当 米时，顶部宽十倍： 或 。我们的方程不是尺度不变的。所描述的形状取决于所使用的单位。

方法 2：外壳

这实际上应该被称为圆柱法。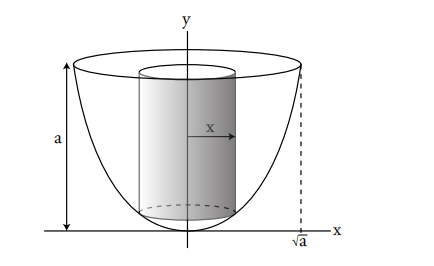

薄外壳/圆柱体的高度为 ，周长为 ，厚度为 。

---

示例 2. 沸腾的坩埚

现在，让我们把水装满这个坩埚，并在下面点燃一把火，让水沸腾（在 ）。
假设这是一个寒冷的日子：坩埚外面空气的温度是 。将水的温度从 升高到 ，需要多少能量才能将水烧开？

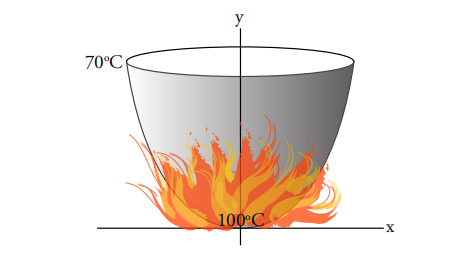
假设温度在坩埚的顶部和底部 之间线性下降：

使用磁盘法，因为水的温度在每个水平磁盘上是恒定的。所需的总热量是

那是多少卡路里？

一块糖果棒大约有 250 千卡，所以大约有

所以，将水烧开大约需要 500 块糖果棒的能量。

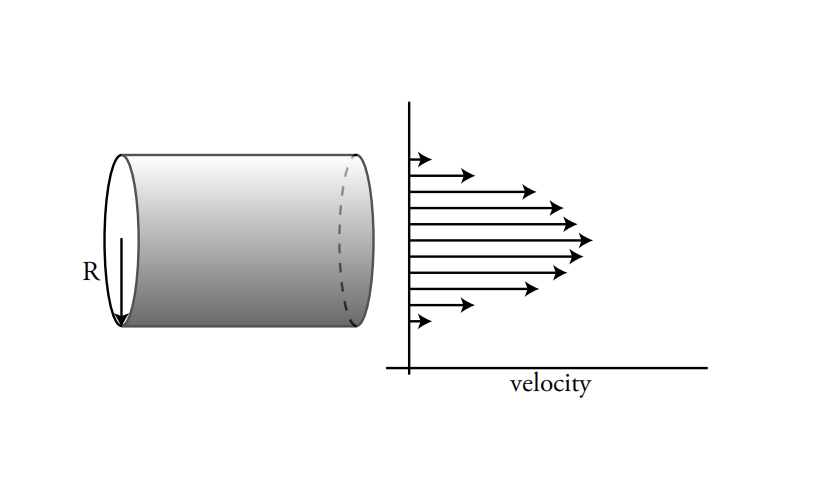
示例 3. 管道流动

泊肃叶是第一个研究流体在管道（动脉、毛细血管）中流动的人。
他发现流体在管道中流动的速度剖面是：

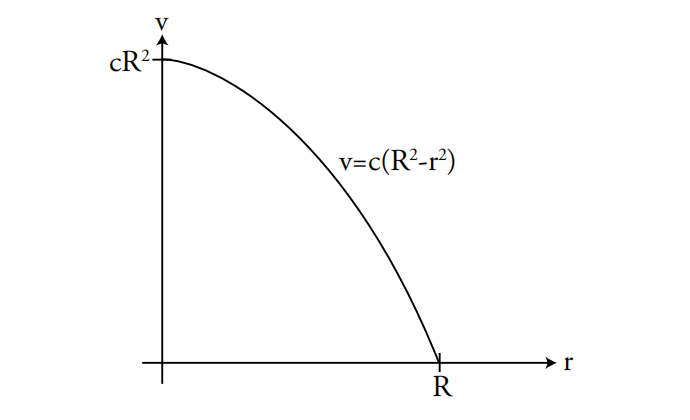
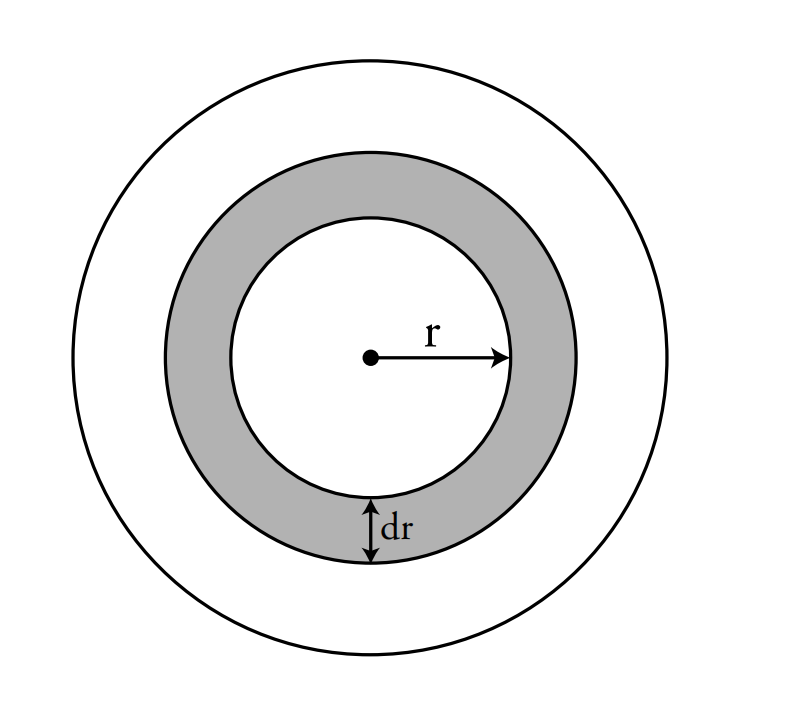
流体流过“环形”的速度是 (环形面积) (流速)
环形面积 (参见图 8：周长 ，厚度 )
类似于外壳的高度。

流过管道的总流量

通过管道的流量

注意，流量与 成正比。这意味着拥有粗管道有很大的优势。

示例 4. 飞镖盘

你瞄准飞镖盘的中心，但你的瞄准并不总是完美的。
在半径 处的命中次数 与 成正比。

这看起来像：

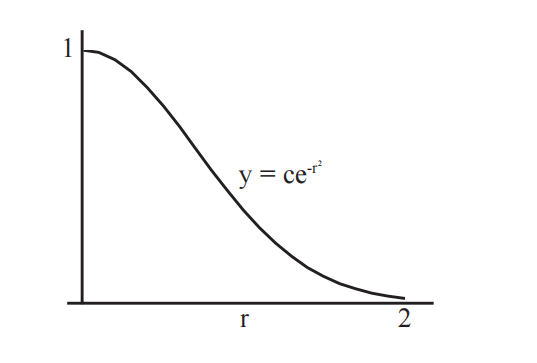
给定环形区域 内的命中次数是

我们将在下一章中更多地研究这个问题。