功、平均值、概率
积分在平均值中的应用
你已经知道如何求一组离散数字的平均值:
现在,我们要求一个连续体的平均值。

这个地方
以及
黎曼和的极限是
除以

例 1. 求
例 2. 常数的平均值就是该常数本身
例 3. 求半圆上相对于弧长的平均高度

例 4. 求上节课女巫坩埚中水的平均温度。(见图 4)。

首先,回顾如何用圆盘法求旋转体的体积。
回想一下
分子是
分母是
因此,平均温度是:
将其与相对于高度
答案
飞镖盘,再次回顾
上次我们说过,你射飞镖的准确性遵循“正态分布”:
现在,让我们假设有人,比如你的小弟弟,愚蠢地决定站在飞镖盘附近。他被飞镖击中的几率是多少?

为了使我们的计算更容易,我们把你的弟弟近似为一个扇形(图 5 中的阴影区域)。
你的弟弟并没有完全站在飞镖盘的前面。让我们说他站在离中心
记住
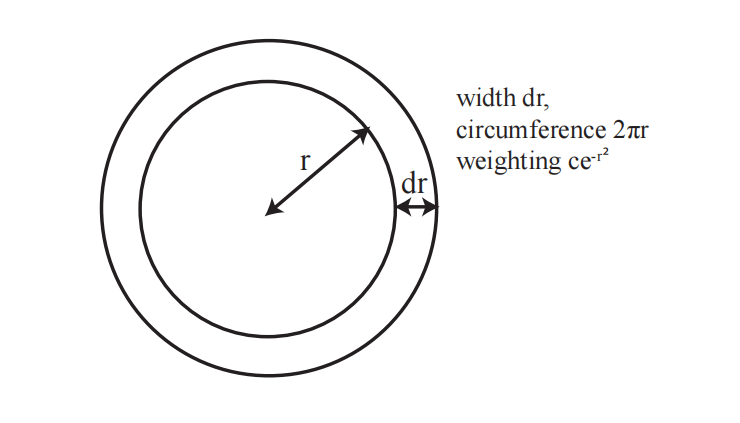
环的权重是
回顾
(
分母:
(注意当

$ 概率=\frac{\frac{1}{6}\int_{2r_{1}}^{3r_{1}}ce^{-r^{2}}2\pi rdr}{\int_{0}^{\infty}ce^{-r^{2}}2\pi rdr}=\frac{\frac{1}{6}\int_{2r_{1}}^{3r_{1}}e^{-r^{2}}rdr}{\int_{0}^{\infty}e^{-r^{2}}rdr}=\frac{1}{3}\int_{2r_{1}}^{3r_{1}}e^{-r^{2}}r~dr $
让我们假设扔飞镖的人大约有一半时间击中飞镖盘
我们得到
所以,被一支飞镖击中你小弟弟的概率约为
换句话说,每扔一支飞镖,他被击中的几率大约是 1%。
通过切片求体积:一个重要的例子
计算
这是微积分中最重要的一些积分之一。它在概率和统计学中尤为重要。
这是一个反常积分,但不要让那些
为了找到
我们通过薄壳法找到这个体积,这会得到与上一个问题相同的积分。
半径为
因此
当
(与飞镖问题中的结果相同)

接下来,我们将用第二种方法,即切片法,来求
沿
由于厚度是
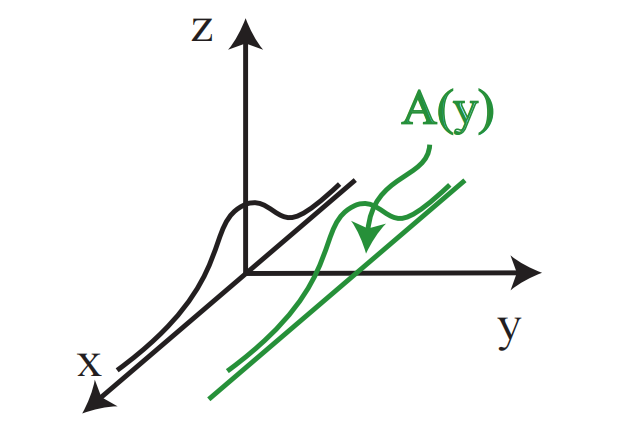
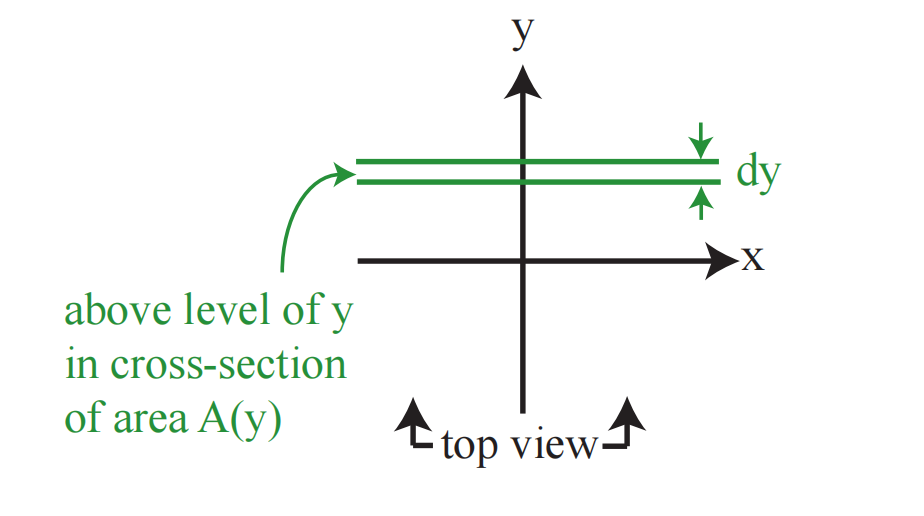
为了计算
在这里,我们使用了
以及在
其中

由此可知
确实,
因为变量的名称不重要。
为了完成计算,请反向阅读等式:
我们可以将
此公式的一个等效缩放版本(用
概率分布
