04-7-数值积分

数值积分

数值积分

我们使用数值积分来求解如下形式的定积分：

当一个积分没有初等不定积分时，我们也求助于数值积分。例如，下面这些就没有公式：

数值积分得到的是数值，而不是解析表达式。
我们将讨论三种数值积分技术：黎曼和、梯形法则和辛普森法则。

1、黎曼和

这里

（或者，）

，

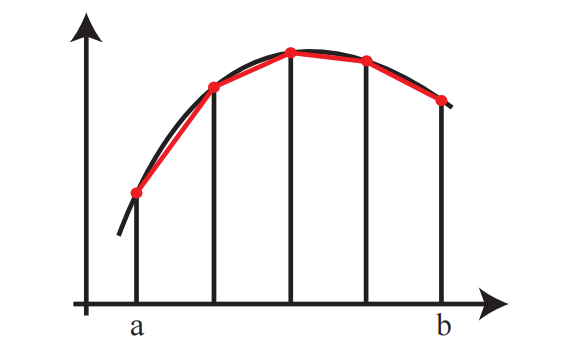
2. 梯形法则

梯形法则将函数下的面积划分为梯形而不是矩形。
梯形的面积是高乘以平行底边的平均值：

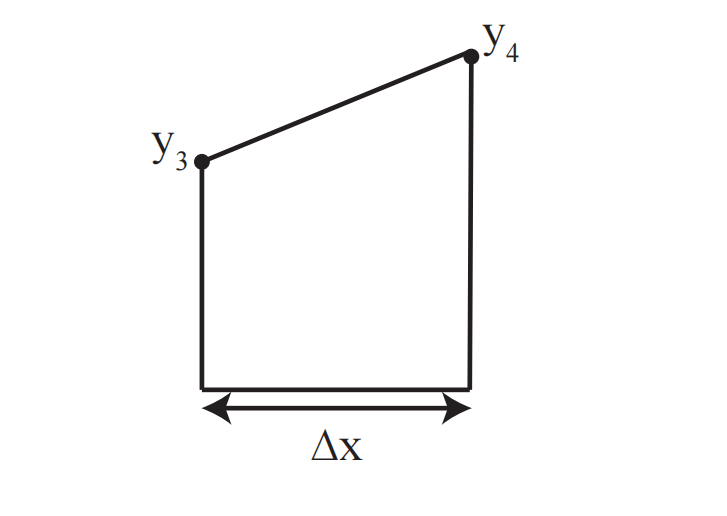
注：梯形法则对两端（ 和 ）的处理比黎曼和更对称——它是左黎曼和与右黎曼和的平均值。

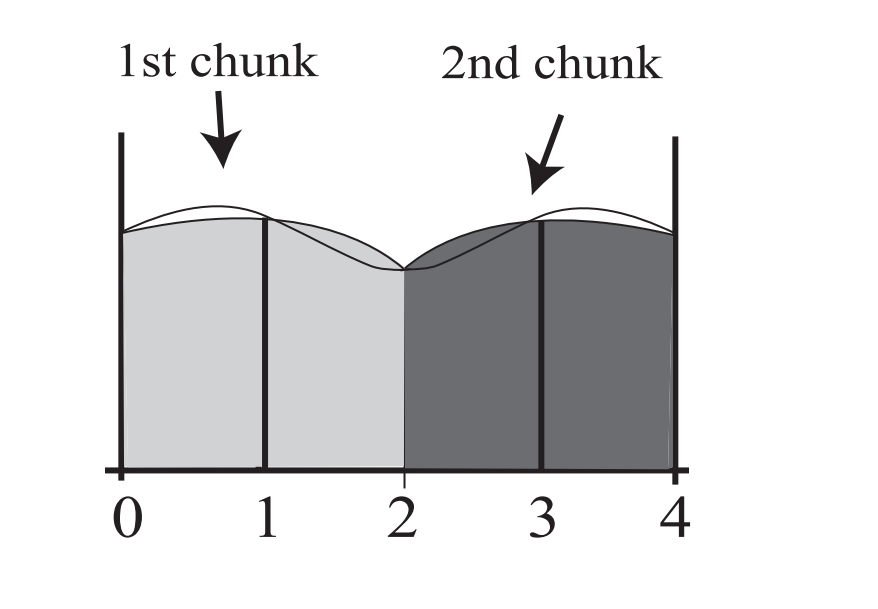
3. 辛普森法则

这种方法通常比梯形法则产生更准确的结果。
在这里，我们将二次函数（即抛物线）拟合到图上，而不是直线或斜线。
这种方法需要偶数个区间。

请注意系数中的以下模式：

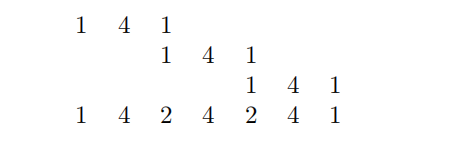
辛普森法则：

括号内系数的模式是：

要再次检查，请代入 （ 偶数！）。

例 1. 使用两种数值积分方法（梯形和辛普森）评估

0	1
1

由梯形法则：

由辛普森法则：

精确答案：

粗略地说，误差，|辛普森 - 精确|，的量级为