01-11-三角函数

三角函数基础

弧度制

在微积分中，我们必须使用弧度制，而不是度数制，因为三角函数的导数和极限公式（比如 的极限）都是基于弧度制推导出来的。

• 定义： 弧长等于半径的中心角大小定义为 1 弧度。
• 换算： 弧度
• 圆上的弧长： 对于半径为 、中心角为 （弧度）的扇形，其弧长
  • 在单位圆 () 中，弧长 就等于角 。（这是理解极限几何证明的关键！）

单位圆与基本三角函数

• 单位圆： 半径为 1、圆心在原点 的圆。
• 对于一个角 ：
  • ： 在单位圆上终点点的 坐标。
  • ： 在单位圆上终点点的 坐标。
  • 勾股定理关系： （即 ）。

三角函数

给定一个三角形：

基于上述关系，我们可以推出三角恒等式：

任意三角函数均已为周期

诱导公式

和角公式

倍角公式

三角有理积分常用的公式

余弦定理

正弦定理

同角关系

万能公式

辅助角公式

例题

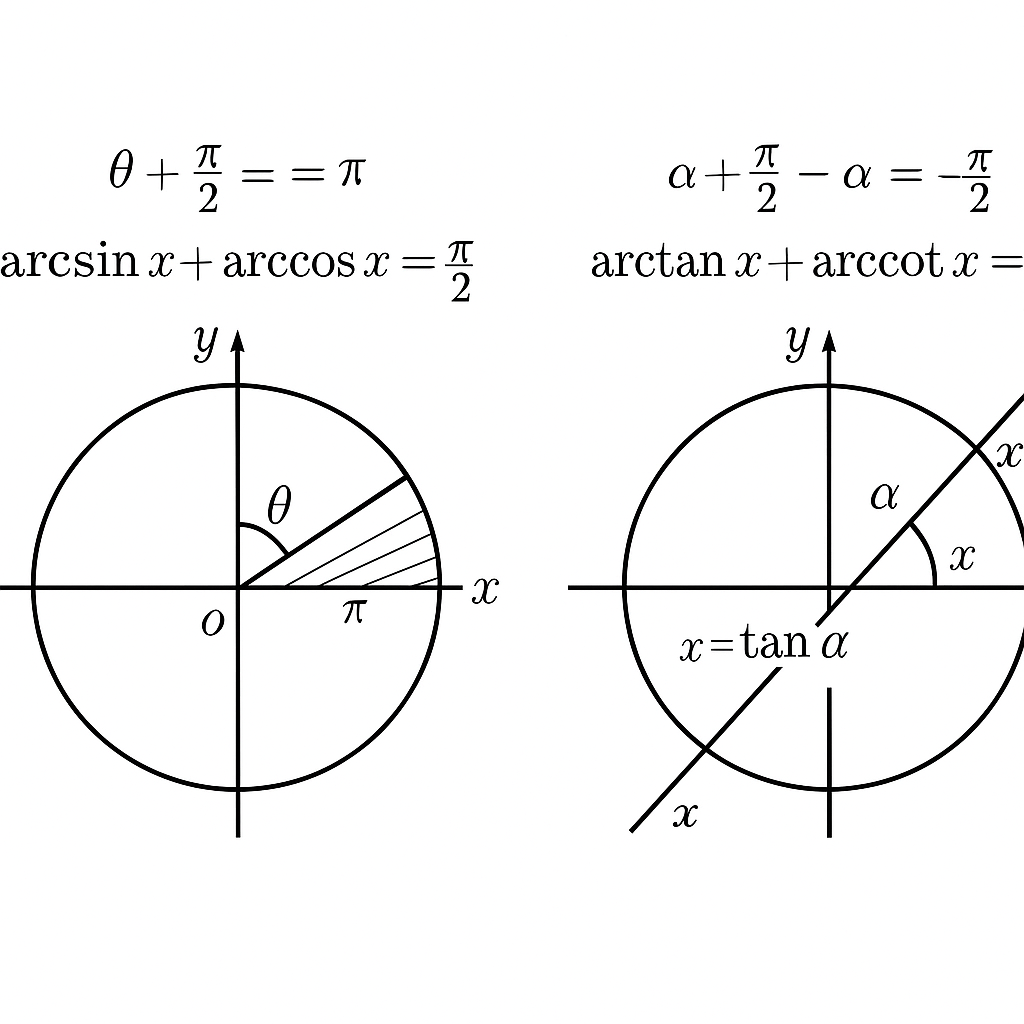
反三角函数

例题2：

数列

• 等差数列：
  • 递推公式：
  • 通项公式：
  • 前n项和：
• 等比数列
  • 递推公式：
  • 通项公式：
  • 前n项和：

数学归纳法

数学归纳法是一种数学证明的方法，通常被用于证明某个命题在自然数范围内成立，其一般步骤如下：

第一步：验证n取第一个自然数时成立

第二步：假设n=k时成立，然后以验证的条件和假设的条件作为论证的依据进行推导，在接下来的推导过程中推导处理在n=k+1时假设的原式成立

最后一步总结表述

例题

例题2:

另一种解题思路