02-1-导数、斜率、速度和变化率

前言

• 什么是导数
  • 几何意义
  • 物理意义
  • 对任何测量都至关重要（经济学、政治学、金融学、物理学等）
• 如何对任何已知的函数求导
  • 例如，今天我们将讨论什么是导数。在此之前，你需要回过头去学习如何对任意函数求导。

第一讲：导数、斜率、速度和变化率

导数的几何视角

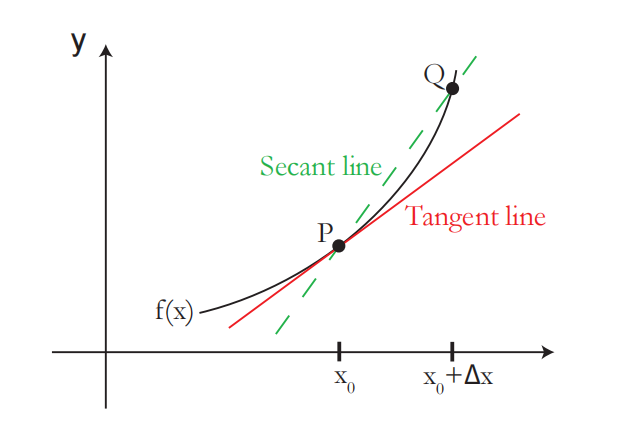
导数是函数图形的切线的斜率。但切线到底是什么呢？

• 它不仅仅是一条与图形相交于一点的直线。
• 它是割线（在图形上的两点之间绘制的直线）的极限，其中这两点之间的距离趋于零。

导数的几何定义：

当 时（ 固定），割线 的斜率的极限。线段 的斜率是：

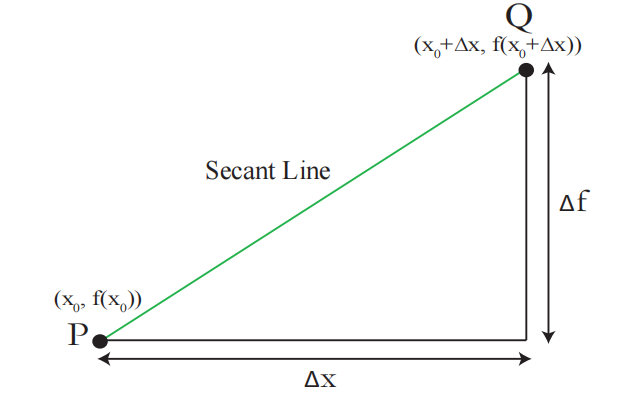
例 1.

在使用导数时需要记住的一点：你可能会想立即代入 。然而，如果你这样做，你将总是得到 。你总是需要进行一些消去才能得到答案。

函数是

将它们代入差商公式：

取 时的极限，这里可以将代入进去可得：

因此，

请注意， 是负数——正如上面图形中切线的斜率一样。
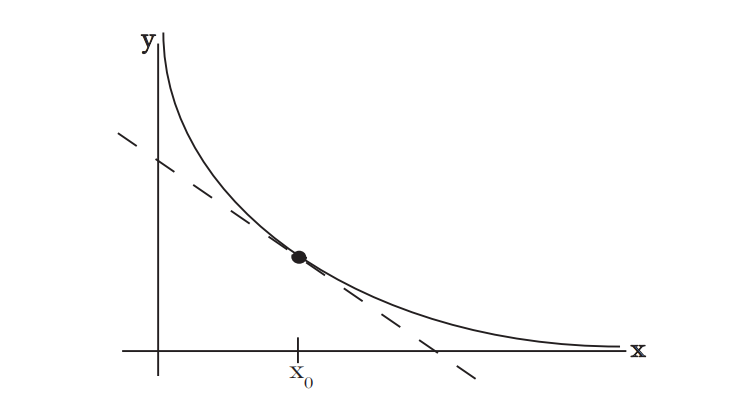
求切线。
利用你们在高中代数中学过的直线方程，写出点 处的切线方程：

代入 和 ，得到：

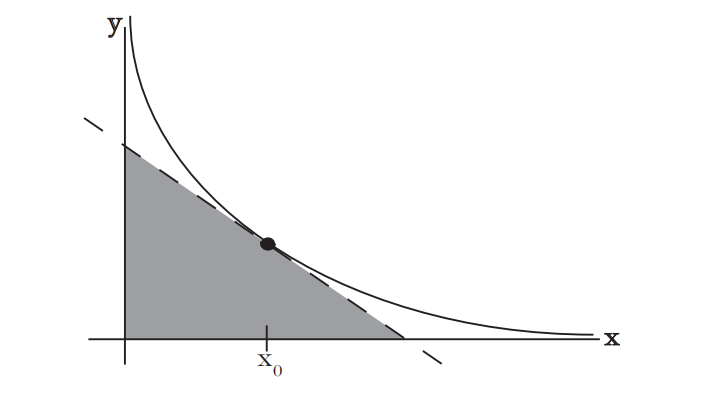
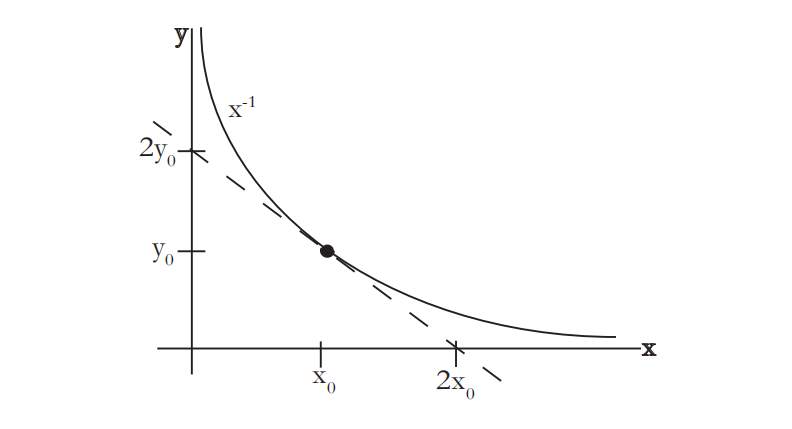
只是为了好玩，让我们计算一下这条切线与 轴和 轴围成的三角形的面积（见图 4 中的阴影区域）。
首先计算这条切线的 截距。 截距是 时的点。将 代入切线方程，得到：

因此，这条切线的 截距位于 处。
接下来我们声称 截距位于 处。由于 和 是相同的方程，所以当 和 互换时，这个图形是关于 直线对称的。根据对称性，则 截距位于 处。如果您不相信这种对称性推理，您可以遵循我们用于求 截距的相同的代数推理链。（请记住，截距是 时的点。）
最后，

奇怪的是，无论我们在图形上的哪个位置画切线，这个三角形的面积总是 2。

记法

微积分，就像英语或任何其他语言一样，是由几位不同的学者发展起来的。因此，正如有很多方式来表达同一事物一样，导数也有很多种记法。
既然 ，很自然地可以写出：

我们称之为 “Delta y” 或 “Delta f”或“的变化量”。
如果我们用 除以等式两边，我们得到差商的两个表达式：

取 的极限，我们得到：

当您使用莱布尼茨（Leibniz）记法时，您必须记住您正在哪个点上求导数——在上面的例子中，是在 处。
用于表示函数 的导数的其他同样有效的记法包括：

（注：，通常用于物理学中的时间导数。）
（注：，是微分算子记法。）

例 2. ，其中

是什么？
为了找到它，将代入差商的定义中：

（从这里开始，我们用 替换 ，以减少书写量。）
因为

---

我们可以将它重写为：

是“所有包含 , 以此类推直到 的项”的简写。（这是被称为二项式定理的一部分）

---

取极限：

---

因此，

---

这个结果可以推广到多项式。例如，

导数的物理解释

您可以将导数视为代表一个变化率（速度就是其中一个例子）。

在万圣节，麻省理工学院（MIT）的学生有一个传统，就是从这栋大约 400 英尺高的建筑屋顶上往下扔南瓜。

（我们暂时接受）地球表面附近物体的运动方程意味着南瓜离地面的高度 为：

当南瓜撞击地面时，，
解得 。因此南瓜需要 5 秒才能到达地面。

平均速度

旁观者可能更感兴趣的是南瓜撞击地面时的速度。为了求出时的瞬时速度，我们来计算 ：

是负数，因为南瓜的 坐标正在减小；它正在向下运动。