极限、连续性与三角函数极限
更多关于导数的“变化率”解释

平均变化率
示例
= 电荷 电流 = 距离 速率(速度) = 温度 温度梯度 - 测量的灵敏度(敏感性):在问题集 1 上进行了一个示例。在 GPS 中,无线电信号给我们提供了
,但存在一定的测量误差(参见图 [2] 和图 [3])。问题是我们能多精确地测量 。为了做出决定,我们找到 。换句话说,这些变量是相互关联的。我们想找出其中一个变量的变化如何影响另一个变量。
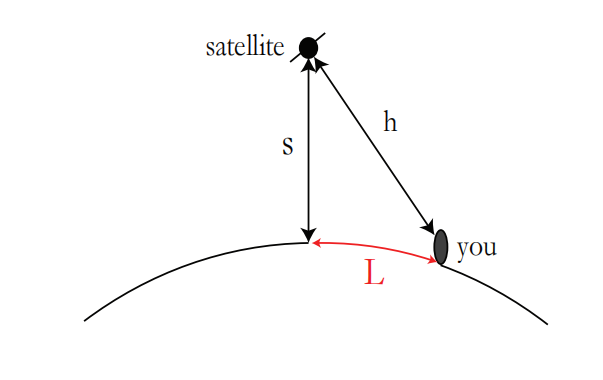
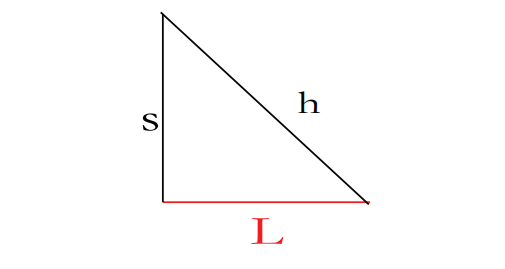
极限与连续性
简单的极限
对于一个简单的极限,你只需代入极限值就可以得到一个有意义的答案。
请记住,
这绝不是一个简单的极限,因为分母
连续性
我们说

这个不连续函数可以在图 [4] 中看到。对于
但是
1.可去不连续点

可去不连续点的定义
右极限:
左极限:
如果
例如,
2.2. 跳跃不连续点

3. 无穷不连续点
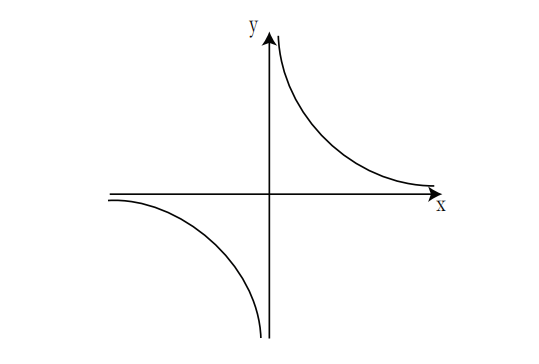
右极限:
左极限:
4. 其它比较恶心的不连续点

这个函数甚至没有趋向于
导数的图像

请注意,函数
南瓜坠落,第二部分
这次,有人将一个南瓜扔过校园里最高的建筑物。


两个三角函数极限
注意:在下面的表达式中,
下面是第一个极限的几何证明:
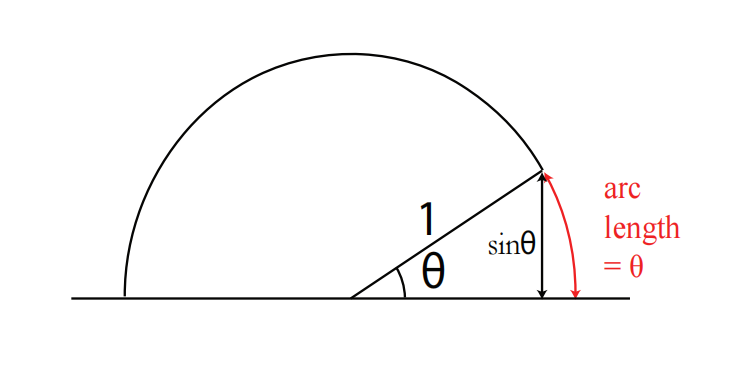
![图 13:图 [12] 中的扇形,当 $ \theta $ 变得非常小时](/../../../images/%E6%95%B0%E5%AD%A6/%E5%BE%AE%E7%A7%AF%E5%88%86/1764211185344-074e5dd6-7906-4604-b59b-edce5984727a.png)
想象一下当
为什么
- 几何理解 (如图 ):
- 当
非常接近 0 时(也就是角变得非常小),我们关注在单位圆中的一个扇形。 是三角形的垂直高(对边)。 是对应圆弧的弧长。 - 当
时,这个三角形的斜边(半径 )几乎与 轴重合,三角形的垂直高 几乎与圆弧的弧长 相等。 - 因此,
趋近于 。 - 结论: 当
时,我们有 。
- 当
涉及余弦的第二个极限呢?
![图 14:与图 [12] 相同的图像,但标记了三角形边缘与圆周之间的水平距离](/../../../images/%E6%95%B0%E5%AD%A6/%E5%BE%AE%E7%A7%AF%E5%88%86/1764211316085-3af6c248-2f79-4459-8def-2a6280e08190.png)
从图 [15] 我们可以看出,当
![图 15:图 [14] 中的扇形,当 $ \theta $ 变得非常小时](/../../../images/%E6%95%B0%E5%AD%A6/%E5%BE%AE%E7%A7%AF%E5%88%86/1764211412211-13ec9b4e-cd46-43f4-9809-7b8e11751e89.png)
2. 为什么
- 几何理解 (如图
): - 当
非常接近 0 时: 是图上红色的水平短线段,它表示半径(长度为 1)与 轴上的投影 之间的极短距离。 是圆弧的弧长。 - 当
时,我们比较 和 这两个无穷小量。 接近 的速度比 更快(它是 的二阶无穷小,即 )。 - 一个更快速趋近于 0 的量除以一个较慢趋近于 0 的量,结果趋近于 0。
- 结论: 当
时, 趋近于 0。
- 当
总结: 掌握了弧度制和单位圆几何关系后,您就可以直观地理解,当角度极小时,
我们以一个定理来结束本次内容,该定理将有助于我们下次计算更多的导数。
定理:可导蕴含连续。
如果
证明:
请记住:你绝不能除以零!第一步是通过乘以
附:为什么乘以
1. 概念回顾:平均变化率
在微积分中,导数是用来测量函数在某一个点的瞬时变化率。
首先,我们从两个点之间的平均变化率(或称为割线斜率)开始:
- 考虑函数
上的两个点: 和 。 和 之间的割线斜率(平均变化率)是:
2. 核心思想:取极限得到瞬时变化率
导数的思想是:我们让第二个点
- 当
趋近于 时,水平距离 趋近于 0,垂直距离 也趋近于 0。 - 这条割线
的极限位置就是函数在点 处的切线。 - 切线的斜率,就是函数在
处的瞬时变化率,我们称之为导数,记为 。
3. 导数的定义式
因此,函数
总结: 当您看到
证明中的应用:为什么变成这样就是导数定义式了?
现在我们回到 可导蕴含连续 的证明:
我们通过代数变形得到了:
根据极限的乘法法则,我们拆分为:
- 左侧的极限: 观察方框中的部分
。 - 对照: 它完全匹配了上面列出的导数定义式。
- 代入: 因为我们已知函数
在 处可导,这意味着这个极限是存在的,并且它的值就是 - 替换: 所以我们用
替换了左侧的整个极限表达式。
这就是证明能够继续进行的关键:通过代数构造,将需要证明的极限 (连续性) 转换成一个包含已知条件 (可导性) 的表达式。
