02-3-乘积、商、正弦、余弦的导数

乘积、商、正弦、余弦的导数

导数公式

导数公式有两种类型：

1. 具体示例： 或
2. 一般示例： 和 （其中 是一个常数）

我们今天将使用的记法约定是：

---

证明 。（一般性）

首先使用导数的定义。

遵循相同的步骤来证明 。

和 的导数。（具体）

上次我们计算了

因此，我们知道了 和 在 处的值。让我们求出它们在任意 处的值。

回顾：

因此，

由于 且 ，上式可简化为

类似的计算可得

乘积法则（一般性）

证明：

显然，

因此，将其加到分子上不会改变任何东西。

我们可以重新排列该表达式得到

请记住，和的极限是极限的和。

注意：我们还用到了以下事实

乘积法则的这个证明假设 和 具有导数，这意味着这两个函数都是连续的。

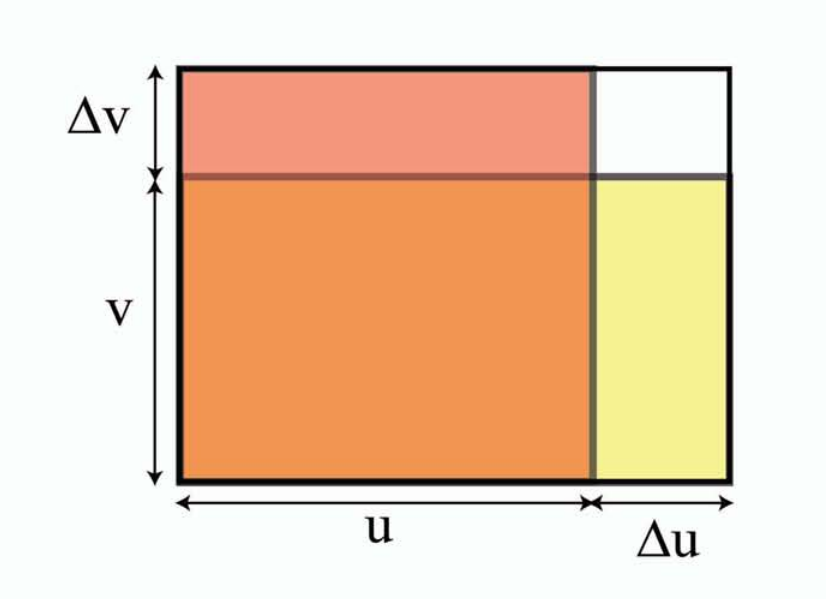
直观的解释：

我们想要求出大矩形和较小的内部矩形之间的面积差。内部的（橙色）矩形的面积为 。定义 为 的变化量，其表达式为

我们还将 简写，使得 ；类似地，。因此，最大矩形的面积是 。

如果让 增加而保持 不变，则增加了红色阴影区域的面积。如果让 增加而保持 不变，则增加了黄色阴影区域的面积。红色和黄色矩形的面积之和为：

如果 和 很小，则 ，也就是说，白色矩形的面积非常小。因此，最大矩形和橙色矩形之间的面积差近似等于红色和黄色矩形的面积之和。因此我们有：

（除以 并令 即可完成论证。）

商法则（一般性）

为了计算 的导数，我们使用上面提到的 和 记法。因此，

因此，

所以，