02-4-链式法则和高阶导数

链式法则和高阶导数

链式法则

我们已经有了对包含加法、减法和乘法的表达式求导的一般程序。那么复合函数呢？

示例 1. ， 。

所以，。为了求 ，写出

由于连续性，当 时， 也趋于 0。所以我们得到：

在这个示例中， 且 。

所以，

链式法则的另一种记法

示例 1.（续） 函数 和 的复合

注意：。不满足交换律！

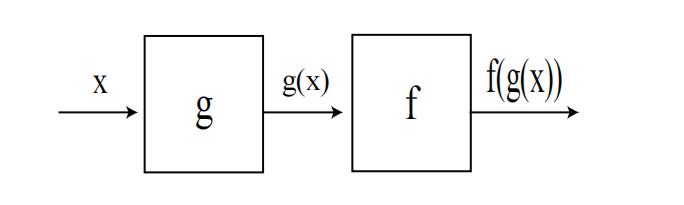
图 1：函数复合：

---

示例 2.

令

示例 3.

有两种方法可以继续。，或

高阶导数

高阶导数是导数的导数。例如，如果 ，那么 是 的二阶导数。我们记作 。

记法

高阶导数非常简单直接——只需持续求导即可！

示例。

从较小的项开始，寻找规律。

记法 称为“n 的阶乘”，定义为 。

归纳证明：我们已经验证了基础情形 ()。

归纳步骤： 假设我们知道 （第 种情形）。证明它对第 种情形成立。

证明完毕！