02-5-隐式微分和逆

隐式微分和逆

隐函数微分法

示例 1. 。

我们通过对 进行显式计算证明了这一点。由此，我们也得到了 的公式。让我们尝试将此公式扩展到涵盖有理数：

令 ；，其中 和 是整数。

我们想要求 。我们可以写成 ，因此 。求解 ：

我们知道 是 的函数。

所以，

这与我们希望得到的结果一致！

示例 2. 半径为 1 的圆的方程：，我们可以写成 。

所以 。让我们看正值情形：

现在，让我们使用_隐函数微分法_来做同样的事情。

在第二项应用链式法则，

相同的结果！

---

示例 3. 。在这种情况下，将 表示为 的函数并不容易。相反，我们使用隐函数微分法来求 。

我们现在可以求解 ，用 和 来表示。

反函数

如果 且 ，我们称 为 的_反函数_，：

现在，让我们使用隐函数微分法来求反函数的导数。

根据链式法则：

且

因此，隐函数微分法使得求反函数的导数成为可能。

示例。

这种形式很复杂。让我们使用一些几何知识来简化它。

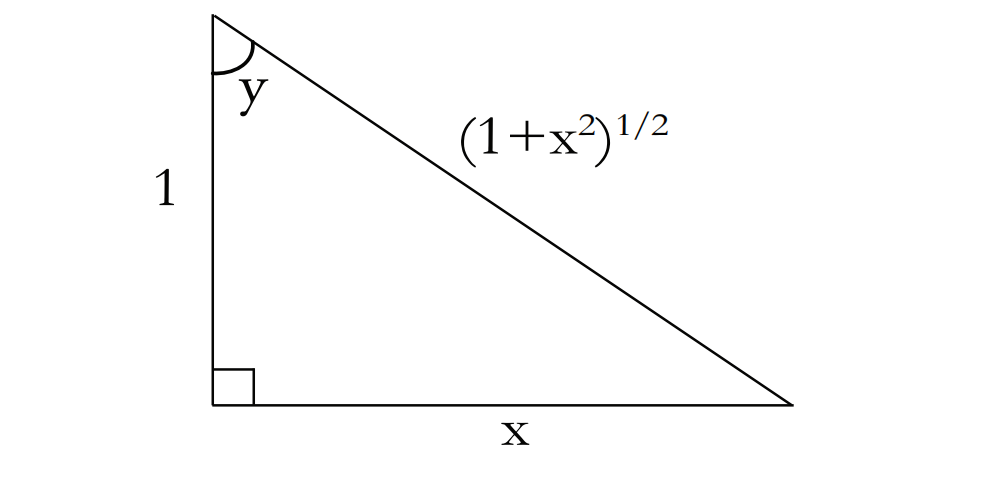
图 1：具有与示例中角度和长度相对应的三角形，用于说明使用反函数 进行的微分

在这个三角形中，，所以

勾股定理告诉我们斜边的长度：

由此，我们可以求出

由此，我们得到

所以，

换句话说，

绘制反函数图。

假设 且 。为了同时绘制 和 的图，我们需要将 写成变量 的函数。如果 ，则 ，我们所做的就是交换变量 和 。如图 2 所示。

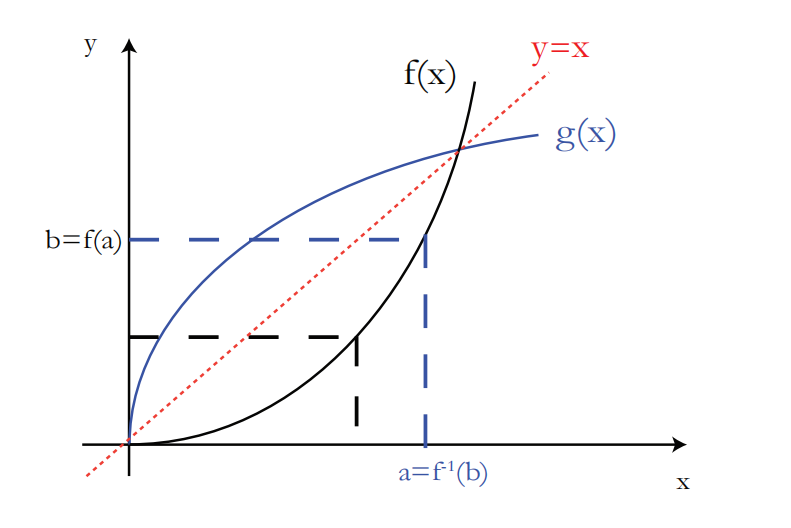
图 2：你可以将视为的图关于直线反射得到的图形