指数和对数、对数微分法、双曲函数
求指数和对数的导数
背景
我们总是假设底数
为了定义实数
今天的主要任务:求
我们可以写成
我们可以提取公因式
我们称
我们尚不知道
这里有两种描述
- 解析上,
在 处的值。
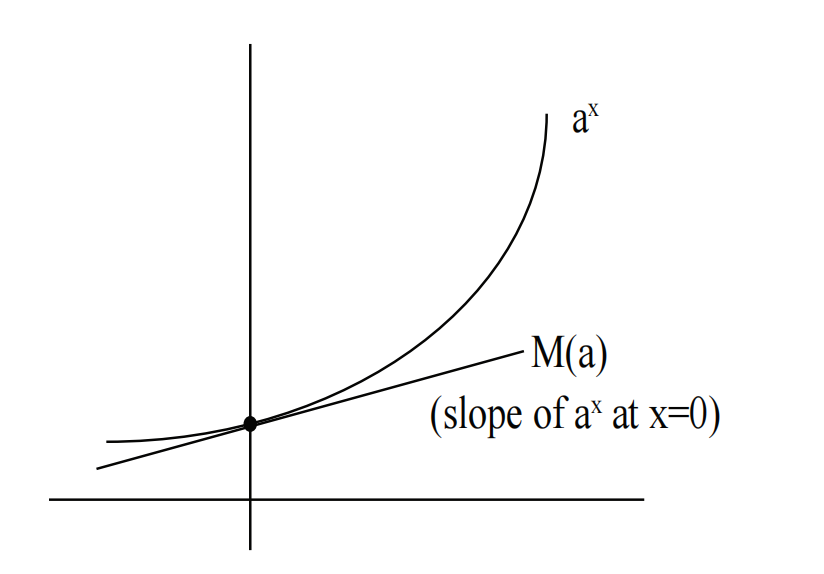
- 几何上,
弄清
接下来,请看图 3 中
在 2 和 4 之间存在一个底数,其在
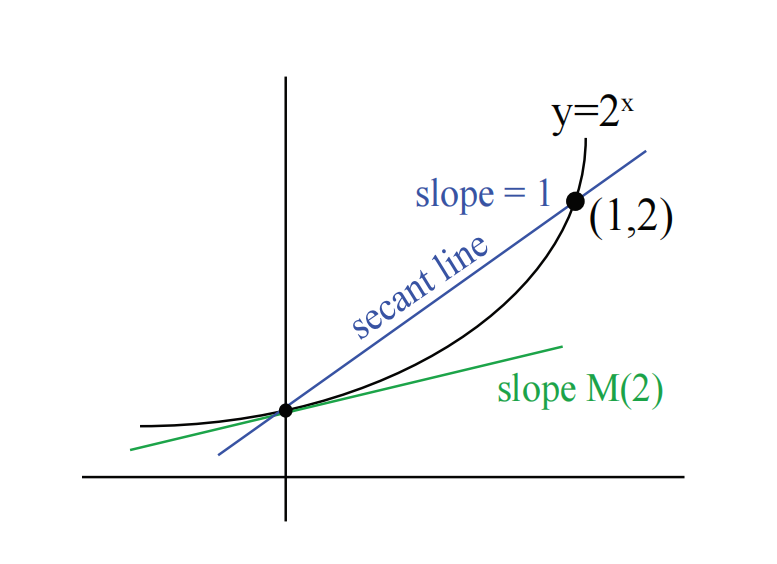

因此,我们可以将
或者,换句话说,
或者,再换句话说,
自然对数(
为了更好地理解
(或)
请注意,即使
回顾
或者,换句话说,
或者,再换句话说,
自然对数(
为了更好地理解
(或)
请注意,即使
回顾
让我们使用隐函数微分法来求
最后,
我们可以使用两种方法:
方法 1:以
将
这看起来可能很难微分。让我们循序渐进:
根据链式法则,
记住,
或
回顾
所以现在我们知道
即使我们坚持从另一个底数(如 10)开始,自然对数仍然会出现:
底数
方法 2:对数微分法。
这个方法的思路是通过求
由于
将此应用于
(记住,
示例 1.
对于带有变量(“移动”)指数的函数,您应该使用底数
因此,
如果您想使用以
链式法则的另一种记法
示例 1.(续) 函数复合
注:
示例 2. 使用对数来计算
因为指数
我们知道
此表达式有两个相互竞争但平衡的部分:
接下来,因为
取极限:当
综上所述,
我们刚刚发现,当
如果
注释 1. 我们从未算出
注释 2. 对数在所有科学甚至金融领域都有应用。想想股票市场。如果我说今天市场下跌了 50 点,你需要知道下跌前的市场平均值是 300 点还是 10,000 点。换句话说,你关心的是百分比变化,或者是变化量与起始值的比率:
