线性和二次逼近
今天,我们将使用微分来进行逼近。
线性逼近
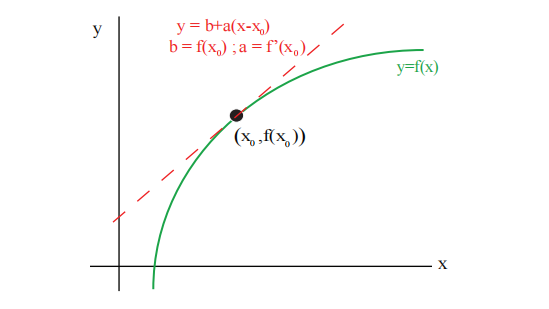
切线逼近函数 。它在切点 附近提供一个很好的逼近。然而,当你远离 时,逼近会变得越来越不准确。
例 1. , (基点)
改变基点:
基点 。
线性逼近的基本列表
在这个列表中,我们总是使用基点 并假设 。
- (如果 )(参见图 2 的 a 部分)
- (如果 )(参见图 2 的 b 部分)
- (如果 )
- (如果 )
- (如果 )
证明
证明 1: 取 ,则 且
因此使用基点 时,。(证明 2, 3 类似。我们已经证明了 4。)
证明 5:
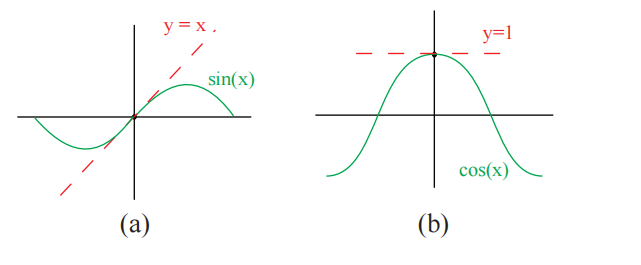
例 2. 求 在 附近的线性逼近。
我们可以计算 并求 。但相反,我们将通过代数组合基本的逼近式来完成。
将这两个逼近式放在一起:
此外,(使用 ,其中 )。
现在,我们丢弃最后一个 (和更高阶)项,因为我们在进行这些逼近时已经舍弃了许多其他的 (和更高阶)项。记住,我们假设 。这意味着 非常小, 甚至更小,等等。我们可以忽略这些高阶项,因为它们非常非常小。
因为 ,我们可以直接从我们的线性逼近中得出 和 ,这比计算 要快。
例 3.
在第一次考试中,你被要求计算 。最快的方法是使用单元 1 的工具,如下所示:
(因为 。在 时,。)
现在我们可以用不同的方式解决相同的问题,使用线性逼近。
因此,
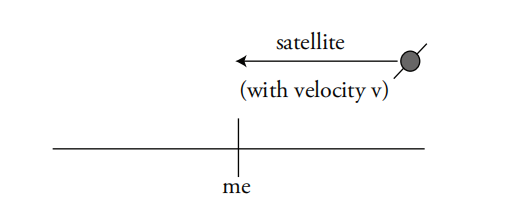
例 4:怪异星球
假设我们在怪异星球上,一个卫星正以极高的速度从我们的头顶呼啸而过。我们想找出时间膨胀(来自狭义相对论的一个概念),即卫星上的时钟相对于我手表上的时钟所经历的时间。我们借用狭义相对论的以下公式:
是卫星上时钟经过的时间, 是我手表上经过的时间, 是卫星的速度, 是光速。
快捷方法到两步过程 是写成:
这里, 是卫星上时钟测量的时间, 是我的手表上测量的时间。我们对这个公式进行线性逼近:
如果 ,光速 ,则 。地面和卫星上的时间差异几乎没有。尽管如此,工程师们仍使用这种逼近(连同其他几个类似的逼近)来校准 GPS 卫星上的无线电发射器。卫星以略微偏移的频率发射。
二次逼近
这些更复杂。它们仅在需要更高精度时使用。
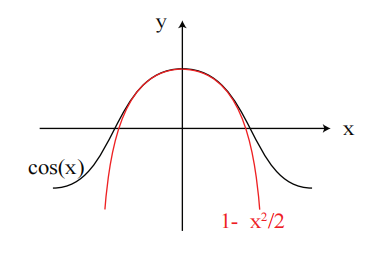
几何图形: 二次逼近给出了一条最适合函数 的抛物线。例如,让我们考虑 (参见图 4)。如果 ,那么 ,且:
你可能想知道 项前面的 是从哪里来的。原因在于对于二次函数,这个逼近是精确的。例如,考虑二次函数:
设定基点 。然后,
0.0.1 基本二次逼近
- (如果 )
- (如果 )
- (如果 )
- (如果 )
- (如果 )
证明: 证明这些公式就是计算每种情况下的 、、。我们来进行第 4 种情况的证明:
现在我们对我们的怪异星球的例子应用二次逼近,看看结果如何。
(使用第 5 种情况,其中 , )
由于 ,所以最后一项将是 数量级。即使是最好的原子钟也无法测量这种精度水平的时间。由于二次项太小了,在这种情况下我们不妨忽略它,并坚持使用线性逼近。
例 5.
让我们求出这个表达式的二次逼近。我们可以将其重写为 。使用每个因子的逼近式,得到:
将这两个多项式相乘,并只保留 和更低阶的项:
(注意:我们丢弃了 和更高阶的项。这是一个二次逼近,所以我们不关心任何高于 的项。)