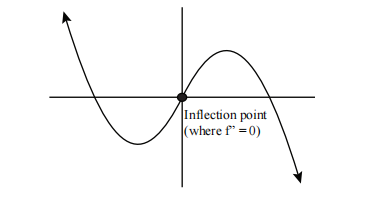
曲线草图
目标: 使用
典型图示:在这里,
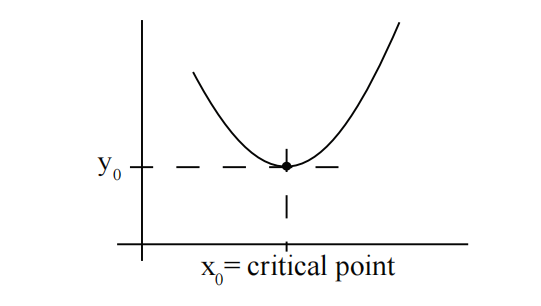
注意,对于
另一种典型图示:在这里,
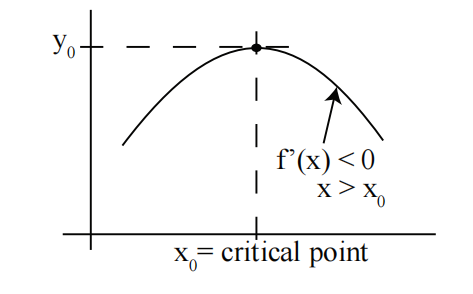
曲线草图绘制的规则
- (预备知识)描绘函数
的不连续点——特别是无穷不连续点! - 找到临界点。这些是
的点(通常是斜率从负变为正,或反之的点)。 - (预备知识)描绘临界点(和临界值),但只有在很容易做到时才这样做。
(a) 决定在临界点之间区域的符号(如果尚未明显)。 - (预备知识)找到并描绘
的零点。这些是使得 的 值。只有在很容易做到时才这样做。 - (预备知识)确定函数在端点(或在
)处的行为。
例 1.
- 没有不连续点。
,所以 在 处。 - (a) 在
处, 。
(b) 在处, 。在图上标记这两个点。 - 找到零点:
,所以零点在 处。 - 函数在
处的行为。
当时, 项占主导地位,所以 。
同样地,当时, 。
将所有这些信息放在一起,我们得到图 3 中所示的图形。
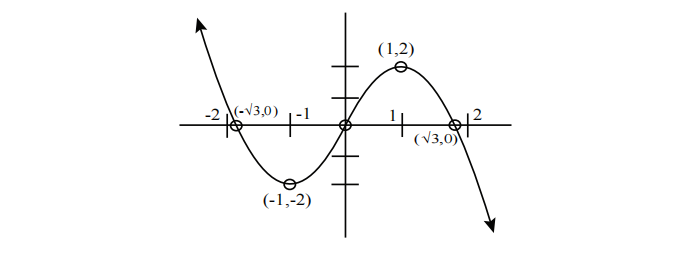
让我们做第 3b 步(
当
例 2.
这个例子说明了在查看函数的导数属性之前,找到函数的不连续点是多么重要。我们计算导数:
警告:导数从不为正,你可能会认为
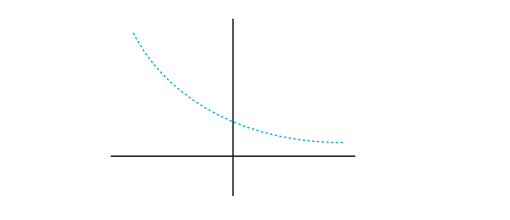
但正如你可能知道的那样,
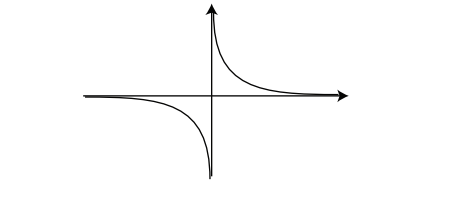
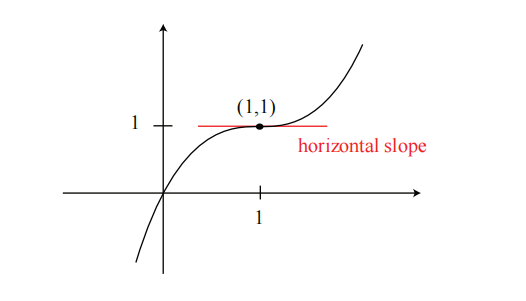
示例 3.
在
示例 4.
(注:此函数仅对
当
换句话说,当
接下来,我们想要求出临界点 (critical points)。
换句话说,临界点是
接下来,求该函数的零点 (zeros):
因此,
当
因此,当
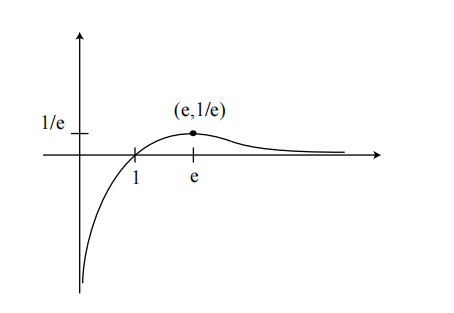
最后,让我们用我们从步骤 3b 得到的信息来核对一下这张图:
果然,该函数在
二阶导数信息
当
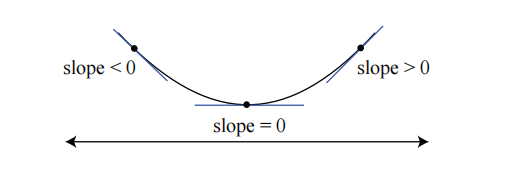
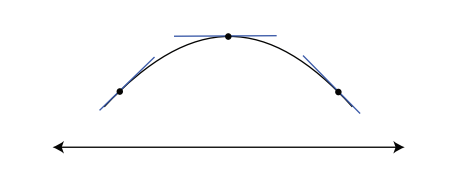
因此,二阶导数的符号告诉我们图线的凹性/凸性。因此,二阶导数主要有两个用途:
- 判断一个临界点是极大值还是极小值。这被称为二阶导数检验法 (second derivative test)。
| 临界点是: | ||
|---|---|---|
| 0 | 负值 (negative) | 极大值 (maximum) |
| 0 | 正值 (positive) | 极小值 (minimum) |
- 凹面/凸面 “修饰 (decoration)”。