03-3-最大值和最小值问题

最大值/最小值问题

例 1. （与上次的文章中的函数相同）

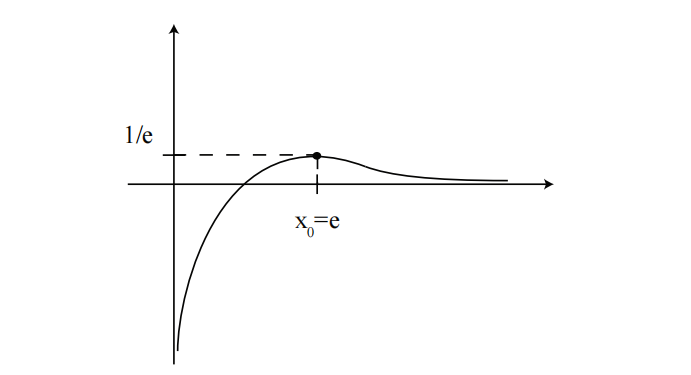
• 最大值是多少？答案：。
• 最大值在哪里（或在哪个点）取得？答案：。（见图 1）

注意： 有些人会问“最大值是多少？”。答案不是 。你可能会习惯于找出临界点 ，这是主要的微积分步骤，但你会忘记找出最大值 。临界点 和临界值 都很重要。它们共同构成了图上的点 ，即函数转折的点。

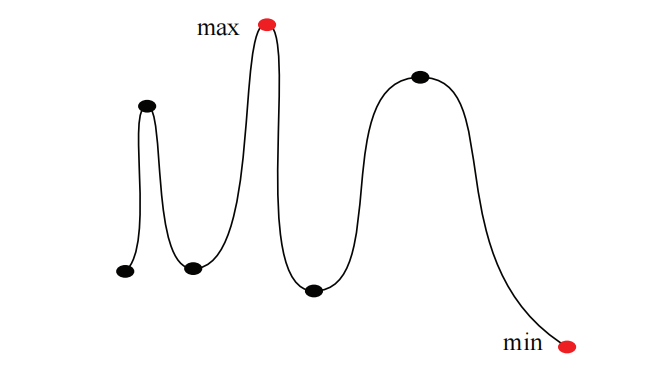
例 2. 找出图 2 中函数的最大值和最小值。

答案： 如果你已经画出函数图，最大值和最小值的值是显而易见的。这里的目标是求出最大值和最小值，无需绘制整个图。

思路： 在临界点和端点中寻找最大值和最小值。你可以从图 2 中看到，我们只需要比较临界点和端点对应的高度或 值。（注意不连续点！）

例 3. 找到一个开口向上的罐子，它能容纳固定的体积 ，但表面积 最小。

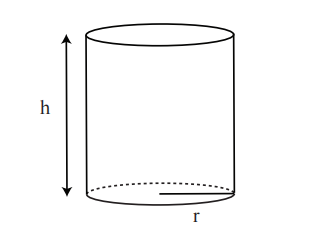
1. 画图。
2. 确定要使用的变量。（在本例中，是 和表面积 。）
3. 确定问题中的约束条件，并用公式表示。在本例中，约束条件是

我们还需要表面积的公式：

现在，用符号表示，问题是在 为常数的条件下，使 最小。

4. 使用约束方程来表达 (以及常数 )：

；

5. 找到临界点（解 ），以及端点。 将在这些位置之一取得最大值和最小值。

我们还没有完成。我们还需要计算端点处的 值： 和 。

当 ，第二项 趋于无穷大，所以 。当 ，第一项 趋于无穷大，所以 。由于 在两个端点处，最小值将在临界点 处取得，而不在任一端点处。

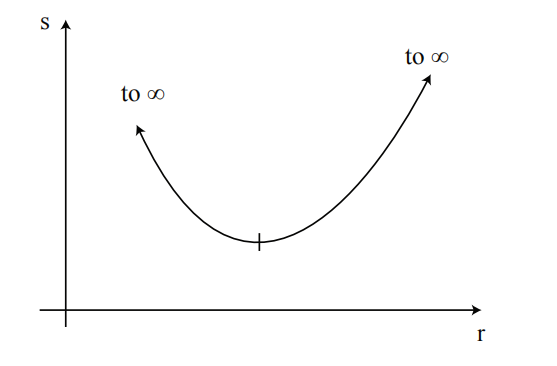
我们仍未完成。我们想找到最小表面积 ，以及 的值。

最后，另一种（通常更好的）回答这个问题的方式是求罐子的比例。换句话说， 是多少？

答案：

示例 4. 考虑一根长度为 1 的电线，将其剪成两段。将每一段弯曲成一个正方形。我们要找出在哪里剪断电线才能使两个正方形围成的总面积尽可能大。

第一个正方形的边长为 。它的面积为 。第二个正方形的边长为 。它的面积为 。因此，总面积为

所以，面积的一个极值是

不过，我们还没有完成。我们还需要检查端点！在 时，

在 时，

通过检查图 6 中的端点，我们看到最小面积是在 处获得的。最大面积不是在 范围内获得的，而是在 或 处获得的。最大值对应于将整根电线用于一个正方形。

启示: 不要忘记端点。如果你只看临界点，你可能会找到最差的答案，而不是最好的答案。