03-4-相关变化率

相关变化率

例1. 警察位于距离路边 30 英尺处。当你的车距离雷达枪 50 英尺时，他们的雷达探测到你的车正以每秒 80 英尺的速度接近。限速为每小时 65 英里（换算后为每秒 95 英尺）。请问你超速了吗？

首先，画出场景示意图（如图 1 所示）：

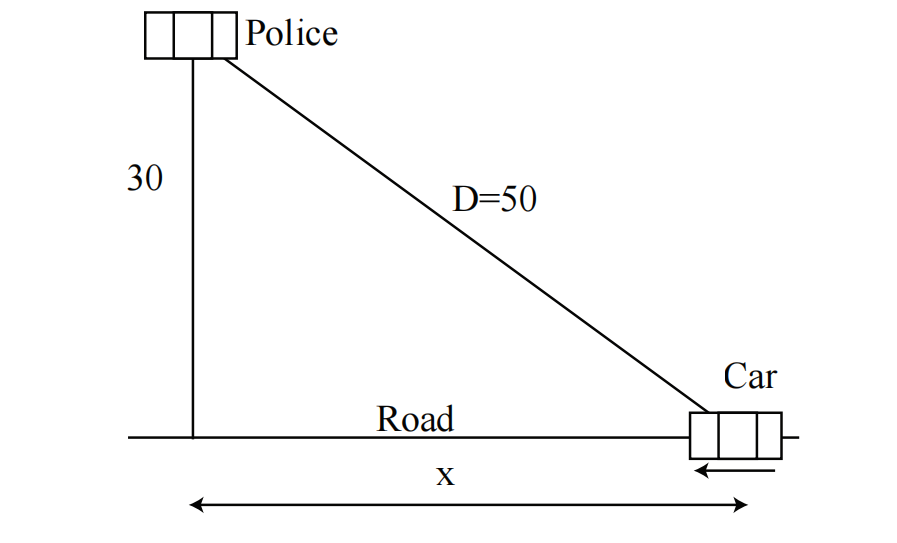
接下来，为变量命名。关键在于确定哪些变量是变化的。

当 时，。（我们要知道这一点，因为这是一个 3-4-5 直角三角形。）此外，。 为负值，因为汽车正朝着 方向移动。切记先不要把 的数值代入！ 是变化的，且它取决于 。

根据勾股定理：

对该方程关于时间求导（隐函数求导）：

现在，代入瞬时数值：

这超过了每秒 95 英尺的限速；实际上，你超速了。

---

解决这个问题还有另一种较长的方法。从以下方程开始：

代入数值：

求解可得：

（第三种策略是对 进行求导。最简单的方法是对代数形式最简单的方程 进行求导，即我们的第一种方法。）

解决这类问题的一般策略是：

1. 画图。设定变量和方程。
2. 求导数。
3. 代入给定数值。切记在求导之后再代入数值。

例2. 考虑一个圆锥形水箱。其顶部半径为 4 英尺，高 10 英尺。水正以每分钟 2 立方英尺的速度注入。当水位高 5 英尺时，水位上升的速度是多少？

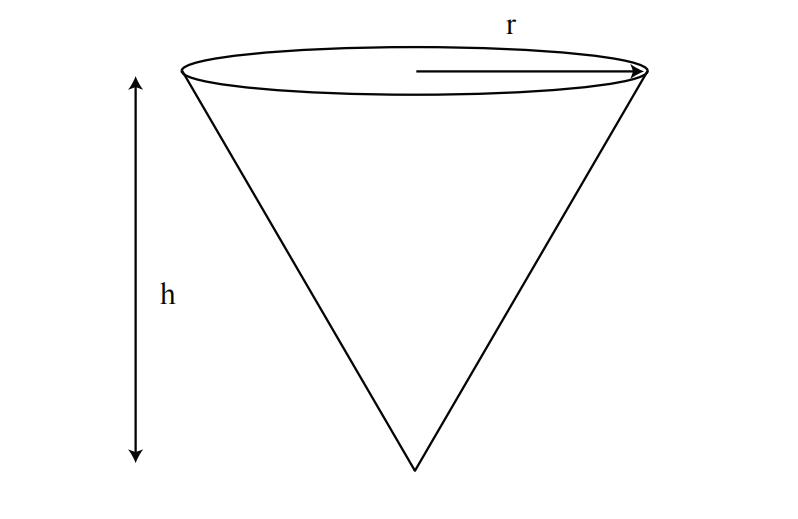
从图 2 中，水箱的体积由下式给出：

这里的关键是画出二维横截面图。我们使用字母和来表示任意水位下的可变半径和高度。我们可以利用图 3 中的相似三角形找到和之间的关系。

图 3：关联 和。

从图 3 中，我们看到

换句话说，

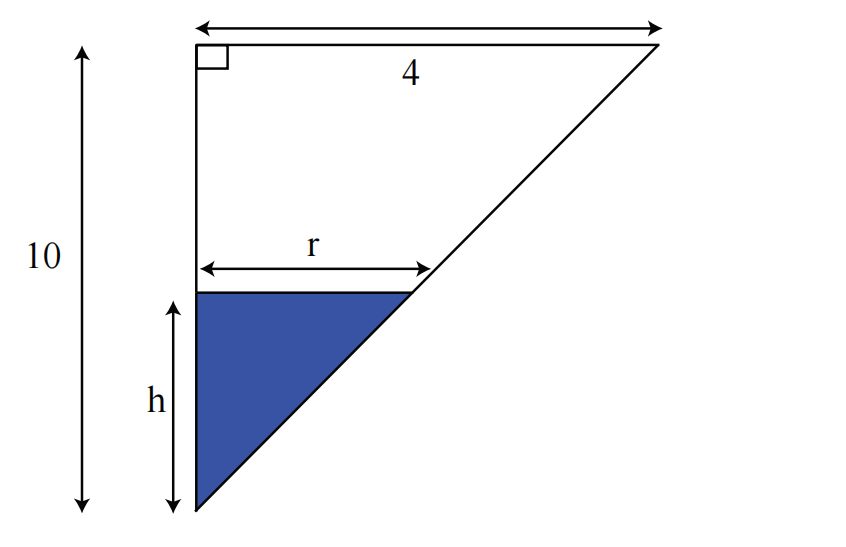
从图 3 中，我们看到

换句话说，

将 的表达式代回 中，得到

对其求导：

现在，代入数值（， ）：

求解得到

相关变化率也出现在问题集 3（图4）中。其中有一个涉及卫星的第二部分误差范围问题，要求你求 。

因此，

还有一个基于类似思想的抛物面镜问题（图 5）。

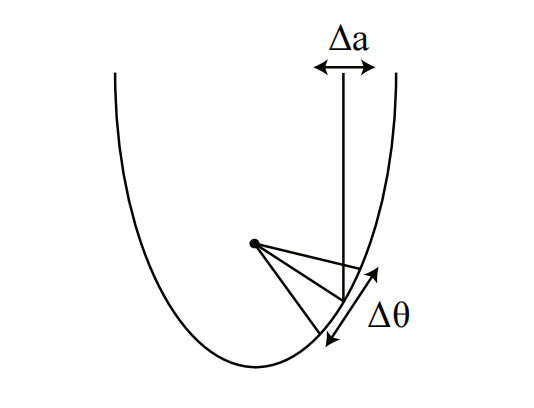
在这里，你需要求。这种测量敏感性问题在每一个测量问题中都很重要，例如预测小行星是否会撞击地球。