03-5-牛顿法及其他应用

牛顿法及其他应用

牛顿法
牛顿法是求解形如 方程的强大工具。
示例 1. 。换句话说，求解 。我们已知这个解是 。牛顿法给出了答案的一个很好的数值近似。该方法利用了切线（见图 1）。

目标是找到图表与 轴相交的位置。
我们从一个猜测值 开始。将其代入 的方程，得到 ，它离 0 还不很近。
我们的下一个猜测是 ，它是函数在 处的切线与 轴相交的位置。
切线的方程是：

当切线与 轴相交时，，所以

记住： 是 在点 处的切线斜率。

用 来表示：

因此，

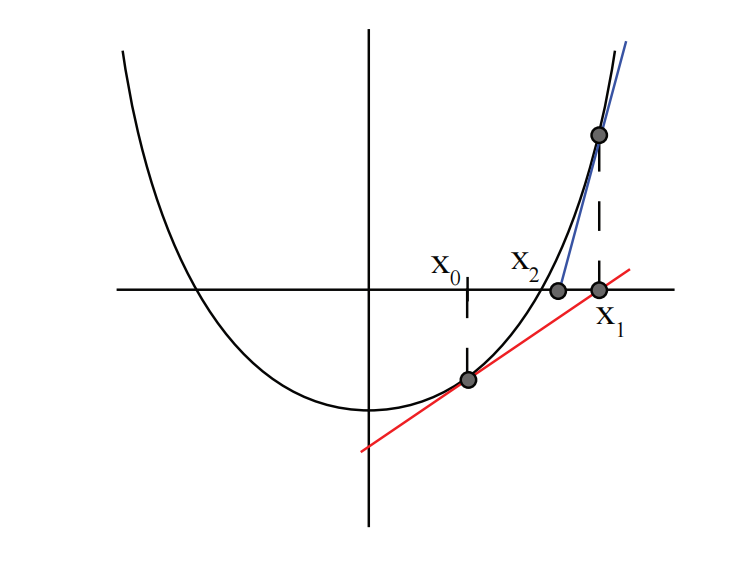
在我们的例子中，。。因此，

主要的想法是重复（迭代）这个过程：

依此类推。该过程对 的近似非常精确。

| 迭代 | 值 | 精度: |
| — | — | — |
| | 1 | |
| | 2 | |
| | | |
| | | |
| | | |

注意，精度的位数随着每次迭代翻倍。
总结
牛顿法如图 3 所示，可以总结为：

示例 1 考虑了如下特殊情况：

现在，我们定义

要在示例 1 中求出 ，取方程的极限，令 。

这得出

这正是我们所希望的：。
警告 1. 牛顿法可能找到意料之外的根。
示例: 如果你取 ，那么 而不是 。这种收敛到意料之外的根的情况如图 4 所示。

警告 2. 牛顿法可能完全失效。
这种失败如图 5 所示。在这种情况下，，，依此类推。它在一个循环中重复，从不收敛到一个单一值。

绳上圆环

考虑一根绳子上的一个圆环，绳子两端固定在 和 处（见图 6）。
圆环可以自由滑动到任何位置。求绳子上圆环的位置 。

物理原理 圆环停留在最低的高度（最低的势能），因此问题是在 位于绳子上的约束下最小化 。

约束 绳子的长度 是固定的：

函数 由上述约束方程隐式确定。我们曾在黑板上描绘了约束曲线（圆环的可能位置）。这条曲线是一个以 和 为焦点的椭圆，但知道它是椭圆并不能帮助我们找到最低点。
对悬挂的圆环的实验表明最低点在中间的某个位置。
由于约束曲线的两端高于中间，最低点是一个临界点（一个 的点）。
在课堂上，我们还通过画出最低点处的水平切线来对这一点进行物理演示。
为了找到临界点，对约束方程关于 进行隐式微分，

由于在临界点处 ，方程可以重写为

从图 6 中，我们看到最后一个方程可以几何解释为

其中 和 是绳子的左半部分和右半部分与垂直方向所成的角度。
物理和几何结论
角度 和 相等。利用向量计算重力施加在绳子两半上的力，可以发现绳子的两半张力相等——这是一个物理平衡。
(从另一个角度看，等角性质表达了椭圆的一个几何性质：假设椭圆是一个镜面。来自焦点 的光线根据入射角等于反射角的规则从镜面反射，因此光线直接射向另一个焦点 。)
和 的公式
我们还没有找到 的位置。我们现在将展示

因为 ，
将以下两个方程相加，

得出

直角三角形的垂直边长方程是（注意 ）：

将这两个方程相加，并使用 ，

使用关系 来写 。那么 的公式是

最后，为了找到 的公式，使用相似的直角三角形

因此，我们得到了用 和 表示 和 的公式。
在文章中省略了 和 的公式推导，因为它很长，而且我们从作为临界点计算的直接结果的平衡条件中，获得了关于这个问题的所有物理直觉和理解。
最后说明. 在单变量微积分中，您将学习使用一种称为拉格朗日乘数的方法来处理任意数量变量的约束最大/最小问题。