03-6-中值定理与不等式

中值定理与不等式

中值定理
中值定理（MVT）是微积分的基础。它阐述了：
如果 在 上可微，并在 上连续，那么

这里，

是割线的斜率，而 是切线的斜率。

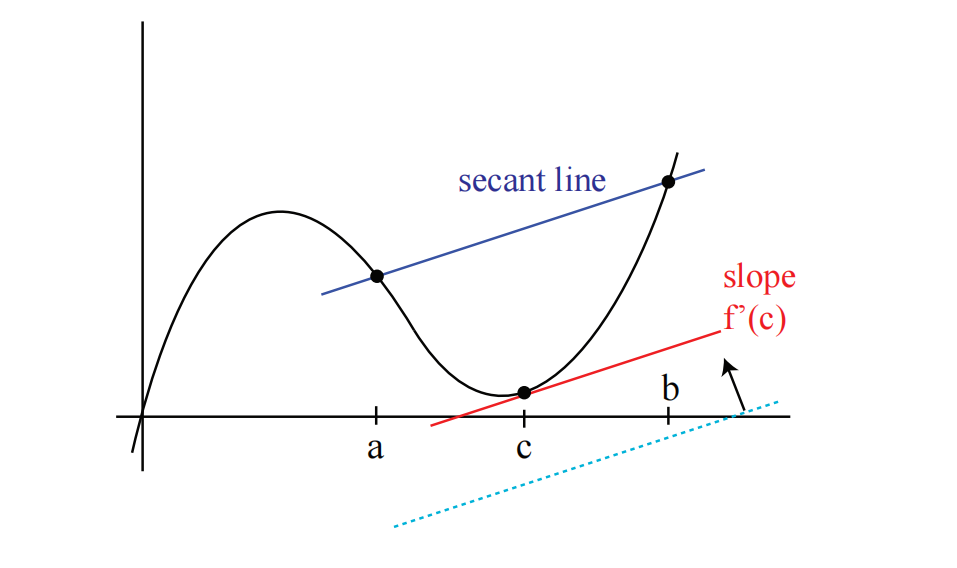
几何证明： 取（虚线）与割线平行的直线，如图 1 所示，并从图形下方向上移动它们，直到其中一条线第一次接触到图形。或者，可能需要从图形上方开始，向下移动虚线直到接触。
如果函数不可微，这种方法就会出错。例如，它对函数 失效。虚线总是首先在 处接触图形，无论其斜率是多少，并且 是未定义的（参见图 2）。

---

中值定理的解释

你在正好 3 小时内从波士顿旅行到芝加哥（我们假设这段旅程为 1,000 英里）。在这两座城市之间的某个时刻，你的速度必然正好是 英里/小时。
位置，以距波士顿的距离衡量。
， ， ， 。

其中 是你在某个时间点 时的速度。
中值定理的各种形式
中值定理还有第二种写法：

中值定理还有第三种写法：将 的名字改为 。

该定理没有说明 是什么。它取决于 、 和 。
应该将这个版本的中值定理与线性近似进行比较（参见图 3）。

线性近似中的切线具有确定的斜率 。相比之下，中值定理公式是一个精确公式。它将缺乏特异性隐藏在了斜率 中，而 可能是 在 和 之间任何一点的斜率。

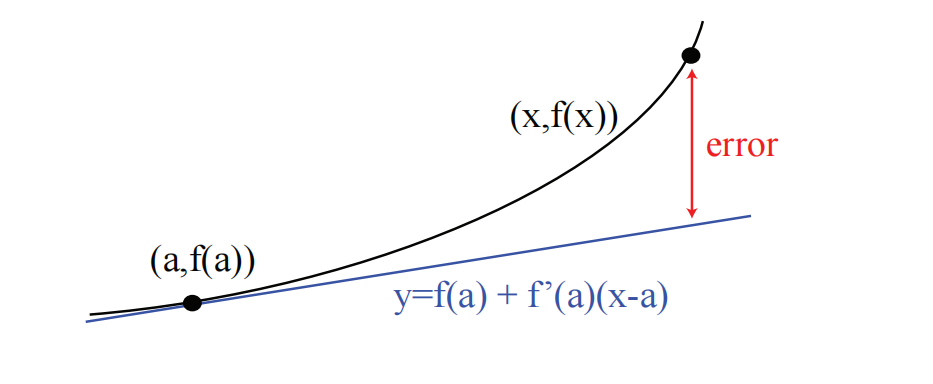
中值定理的应用。
关键结论：（中值定理的结论是理论性的）

1. 如果 ，那么 是递增的。
2. 如果 ，那么 是递减的。
3. 如果对所有 都有 ，那么 是常数。
   递增/递减的定义：
   递增意味着 递减意味着 。
   证明：
   证明 1：
   

4. 因为 和 都为正，

5. （证明 2 被省略，因为它与证明 1 相似）
   证明 3：

6. 结论 1、2 和 3 看起来很明显，但请允许我让您相信它们并非如此。回顾导数的定义。它涉及无穷小量。这些无穷小量与函数的非无穷小行为有什么关系，这并非是确定无疑的。
   3

— 页面 5 —

第 14 讲
18.01 2006 年秋季
不等式
基本性质 递增可用于推导许多其他不等式。
示例。

2. 对于
3. 
   证明。 我们将属性 1 视为已知。其他两个属性的证明如下：
   证明 2：定义 那么， 且 （最后一个断言来自第 1 步）。
   因此， 是递增的，所以对于 有 。即：

4. 证明 3：令
   。这是 。 (如果 )。
   因此， 对于 。换句话说，

5. 类似地，（使用 证明）
   可以继续推导：

6. 最终证明

7. 当我们在课程临近结束时学习泰勒级数时，我们将讨论这一点。
   4