03-8-微分方程和变量分离

微分方程与分离变量法

常微分方程 (ODEs)

• 例 1.
  • 解： 我们认为这类方程已求解。
• 例 2.
  • （ 在量子力学中被称为湮灭算符。）
  • 到目前为止，除了积分，我们只有一种方法来解它，即代换。求解 得到：
  • 关键步骤是分离变量。
  • 请注意，所有 相关的项都在左侧，所有 相关的项都在右侧。
  • 接下来，对两边取反导数：
  • （只需要一个常数 ）
  • （取指数）
  • （）
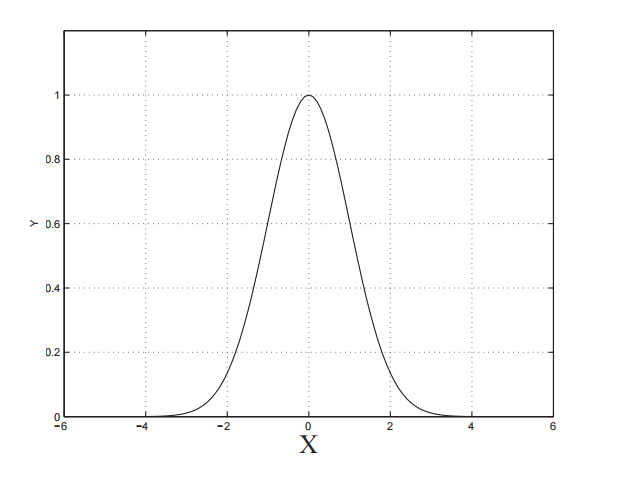
  • 尽管 成立，但 是可能的，以及所有 ，这取决于初始条件。
  • 例如，如果 那么 。如果 那么 （见图 1）。

一般情况：

• 我们可以写成 (其中 。)
• 现在，我们得到 的一个隐式公式：
• (其中
• 其中 , 并且
• （ 是反函数。）
• 在前面的例子中：

例3（几何示例）。

找到一个图形，使其切线的斜率是连接原点 到点 的射线的斜率的两倍（如图 2 所示）。

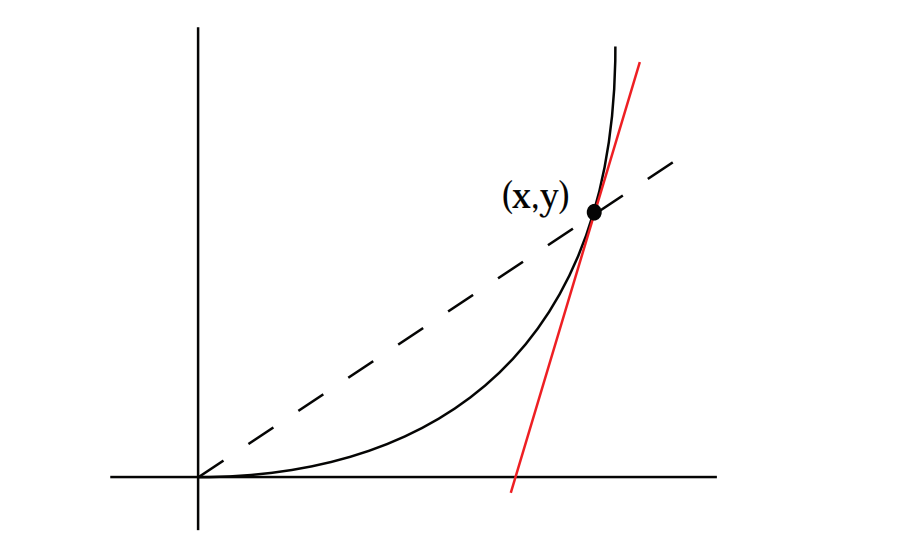
因此，

（分离变量）

（反导数）

（取指数；请记住，

同样， 、 和 都是可接受的。可能的解包括，例如，

例 4。 找到垂直于例 3 中抛物线的曲线。

我们知道它们的斜率是，

分离变量：

取反导数：

这是一个椭圆族的方程。对于这些椭圆， 半长轴与 半短轴的比率为 （见图 3）。

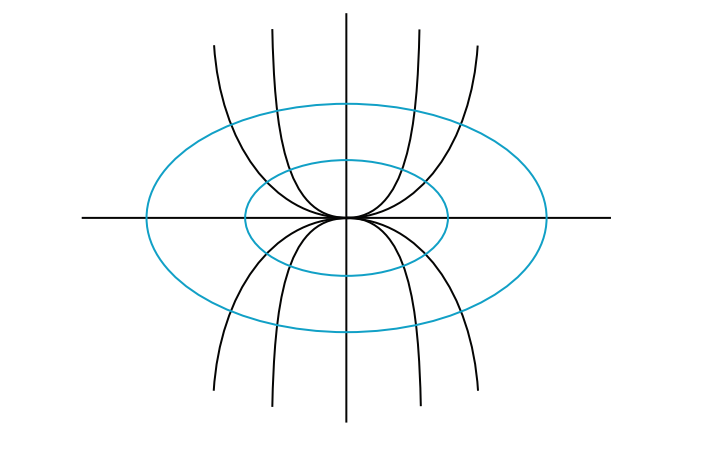
分离变量法导致 的隐式公式，但在这种情况下，你可以解出 。

往期回顾

1. 线性和/或二次近似。
2. 的草图。
3. 最大值/最小值问题。
4. 相关变化率。
5. 反导数。分离变量法。
6. 中值定理。