04-1-定积分

定积分

积分可用于计算累计总量、平均值和面积。

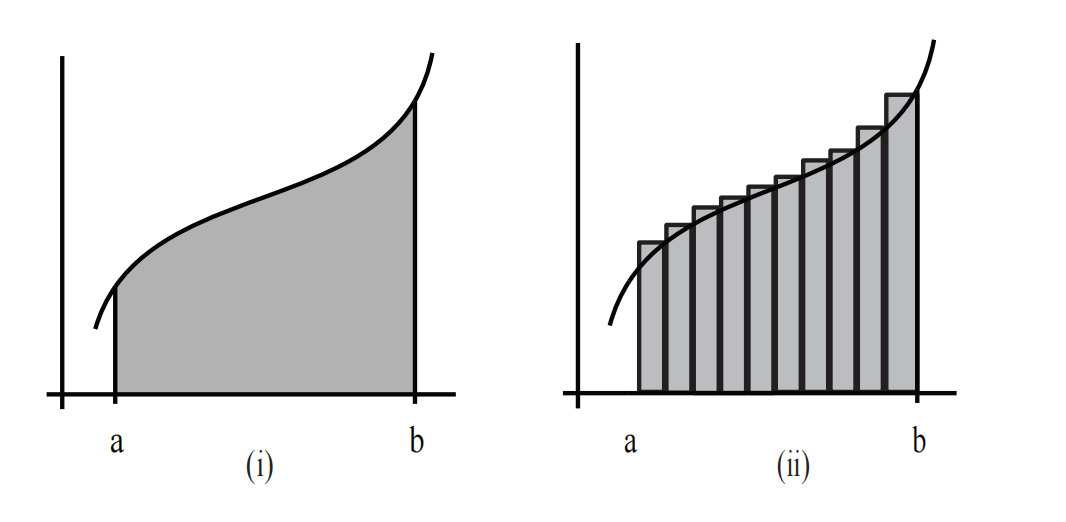
曲线下的面积：(见图 1。)

1. 将区域划分为矩形
2. 将矩形的面积相加
3. 取矩形变薄时的极限

例 1. 任意

1. 分成 个区间
   长度 矩形的底
2. 高度：
   • : -高度
   • : -高度

矩形面积的和:

我们现在将使用一些三维几何知识来估算这个和。
考虑如图 3 所示的阶梯金字塔。

层: 底部，表示体积 。
层: ，表示体积 等。
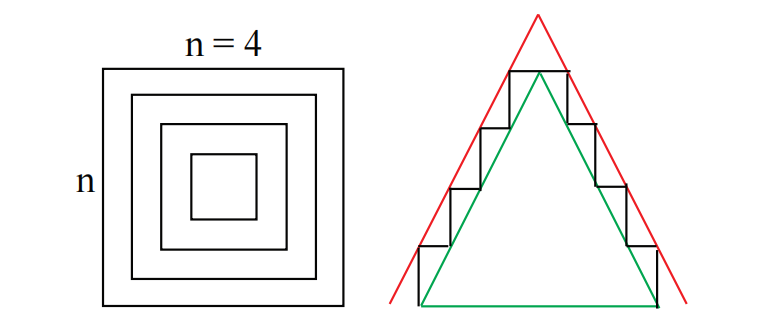
因此，阶梯金字塔的总体积是

接下来，金字塔的体积大于内部棱柱的体积:

且小于外部棱柱的体积:

总而言之:

因此，

在 0 到 之间的面积是

例 2. ; 在 上方的面积。与例 1 相似，但更简单的推理给出面积之和:

这是图 4 中三角形的面积。

模式:

下方的面积 应该满足 。

一般情况

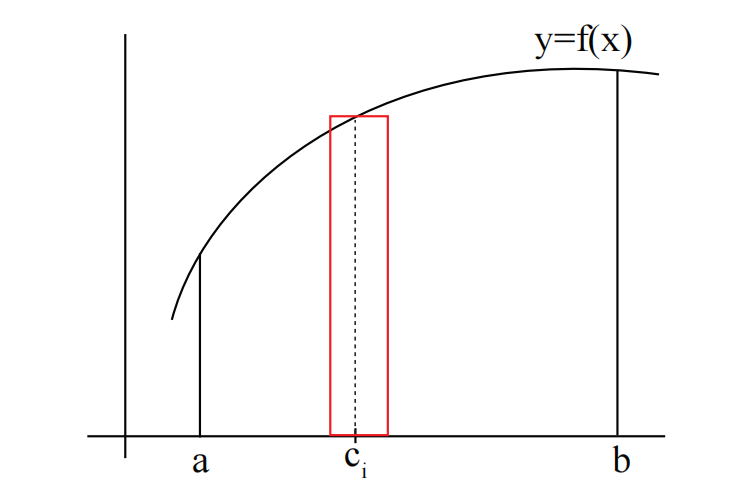
• 分成 个等长小块
• 在区间内任取一个 ; 使用 作为矩形的高度
• 面积之和:

用求和符号表示: 称为黎曼和。

定义:

称为定积分。

这个定积分表示曲线 在 上方的面积。

例 3. (积分应用于面积以外的数量。) 学生向父母借款。
本金 (美元)， 时间 (年)， 利率 (例如，6% 是 )。
在时间 之后，你欠 。

积分可以用来表示借款总额，如下所示。
考虑一个函数 ，以美元/年计的“借款函数”。
例如，如果你借 ，则 。允许 随时间变化。
假设 。

是第 个月期间的借款率，所以借款金额是 总额是

当 时取极限，我们得到

这表示一年内借款总额 (以美元/年计)。

积分也可以用来表示总欠款。总欠款取决于利率。
你在时间 借款所欠的金额是

年底借款总欠款是